Measurement with the Light Microscope

Your microscope may be equipped with a scale (called a reticule) that is built into one eyepiece. The reticule can be used to measure any planar dimension in a microscope field since the ocular can be turned in any direction and the object of interest can be repositioned with the stage manipulators. To measure the length of an object note the number of ocular divisions spanned by the object. Then multiply by the conversion factor for the magnification used. The conversion factor is different at each magnification. Therefore, when using a reticule for the first time, it is necessary to calibrate the scale by focusing on a second micrometer scale (a stage micrometer) placed directly on the stage.

Conversion factor

Identify the ocular micrometer. A typical scale consists of 50 - 100 divisions. You may have to adjust the focus of your eyepiece in order to make the scale as sharp as possible. If you do that, also adjust the other eyepiece to match the focus. Any ocular scale must be calibrated, using a device called a stage micrometer. A stage micrometer is simply a microscope slide with a scale etched on the surface. A typical micrometer scale is 2 mm long and at least part of it should be etched with divisions of 0.01 mm (10 µm).

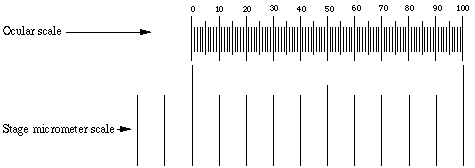
Suppose that a stage micrometer scale has divisions that are equal to 0.1 mm, which is 100 micrometers (µm). Suppose that the scale is lined up with the ocular scale, and at 100x it is observed that each micrometer division covers the same distance as 10 ocular divisions. Then one ocular division (smallest increment on the scale) = 10 µm at 100 power. The conversion to other magnifications is accomplished by factoring in the difference in magnification. In the example, the calibration would be 25 µm at 40x, 2.5 µm at 400x, and 1 µm at 1000x.

Some stage micrometers are finely divided only at one end. These are particularly useful for determining the diameter of a microscope field. One of the larger divisions is positioned at one edge of the field of view, so that the fine part of the scale ovelaps the opposite side. The field diameter can then be determined to the maximum available precision.

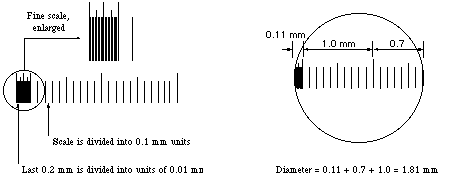
Estimating and reporting dimensions

Be aware that even under the best of circumstances the limit of resolution of your microscope is 1 or 2 µm (or worse) at any dry magnification, and 0.5 µm or so using oil immersion. No directly measured linear dimension or value that is calculated from a linear dimension should be reported with implied accuracy that is better than that. That includes means, surface areas, volumes, and any other derived values. For example, suppose you measure the length of a flagellum on a Chlamydomonas cell at 400x, and determine that it covered 3 1/2 ocular divisions. The length is directly calculated as 3.5 divisions times 2.5 µm per division, which comes out to 8.75 µm. You know, however, that at 400x the absolute best you can do is to estimate to the nearest µm, so before reporting this measurement round it to 9 micrometers (not 9.0, which would imply an accuracy to the nearest 0.1 µm). For more information on reporting uncertain quantities see our Resources section (analytical resources).

The calculation of a volume is subject to error propagation, namely the magnification of an error when deriving a figure from one or more measured variables. For example, suppose you measure the length and diameter of an object to be 65 and 30 micrometers, respectively, assuming a cylindrical shape. The volume is given by the formula v = ¼r2l, where r = radius and l = length. The formula gives a volume of 45, 946 µm3. The volume isn't accurate to the nearest cubic micrometer, however.

Let's make the very optimistic assumption that the measurement of 65 micrometers is indeed accurate to the nearest 1 µm. Then the number 65 means "greater than 64.5 and less than 65.5." The number 30 really means "greater than or equal to 29.5 and less than or equal to 30.5." The smaller set of measurements yields a volume of 44,085 µm3, while the larger yields a volume of 47,855 µm3. False precision would be implied even if one reported a volume of 46,000 µm3, obtained by rounding the middle measurement. It would probably be better to report a range in this case, of 44,000 to 48,000 µm3. By the way, 46,000µm3 is 0.046 mm3, which probably represents a better choice of units in this case.

Making assumptions

In many areas of experimental science, including biosciences, the ability to estimate and make reasonable assumptions is a valuable skill. In order to make some quantitative estimates, particularly of volumes, you will have to make assumptions regarding the shape of some organisms. For example, if a specimen appears round, you would likely make your volume calculation based on the assumption that the specimen is a perfect sphere. For something like a Paramecium you might assume a cylindrical shape in order to simplify your estimate, while remaining aware that you could be way off the mark.

A specimen such as Chaos (Pelomyxa) carolinensis represents a real challenge. Ameoboid organisms are irregularly shaped most of the time. Is it flat on the slide, or does it extend up toward the coverslip? Perhaps it is attached to both. What model do you use as a basis for volume estimation? Is it best to assume a particular shape and take measurements at different times? Is it best to estimate a maximum and minimum for each possible dimension and obtain a range of possible volumes? Remember, you are only asked to estimate. Sometimes the best estimates have a potential error of more than an order of magnitude.