Experimental error: Under "Analytical resources," review "error analysis and significant figures" and "error representation and curvefiting."
Statistical tests: [Unpaired (independent) t test] [paired t test] [Chi-squared test] [sample problems] [solutions to sample problems]
Tables: ['Student's' t distribution] [Chi-squared critical values]

'Student's' t Test (For Independent Samples) Use this test to compare two small sets of quantitative data when samples are collected independently of one another. When one randomly takes replicate measurements from a population he/she is collecting an independent sample. Use of a paired t test, to which some statistics programs unfortunately default, requires nonrandom sampling (see below). Criteria Only if there is a direct relationship between each specific data point in the first set and one and only one specific data point in the second set, such as measurements on the same subject 'before and after,' then the paired t test MAY be appropriate. If samples are collected from two different populations or from randomly selected individuals from the same population at different times, use the test for independent samples (unpaired). Here's a simple check to determine if the paired t test can apply - if one sample can have a different number of data points from the other, then the paired t test cannot apply. Examples 'Student's' t Test is one of the most commonly used techniques for testing a hypothesis on the basis of a difference between sample means. Explained in layman's terms, the t test determines a probability that two populations are the same with respect to the variable tested. For example, suppose you collected data on the heights of male basketball and football players, and compared the sample means using the t test. A probability of 0.4 would mean that there is a 40% liklihood that you cannot distinguish a group of basketball players from a group of football players by height alone. That's about as far as the t test or any statistical test, for that matter, can take you. If you calculate a probability of 0.05 or less, then you canreject the null hypothesis (that is, you can conclude that the two groups of athletes can be distinguished by height. To the extent that there is a small probability that you are wrong, you haven't proven a difference, though. There are differences among popular, mathematical, philosophical, legal, and scientific definitions of proof. I will argue that there is no such thing as scientific proof. Please see my essay on that subject. Don't make the error of reporting your results as proof (or disproof) of a hypothesis. No experiment is perfect, and proof in the strictest sense requires perfection. Make sure you understand the concepts of experimental error and single variable statistics before you go through this part. Leaves were collected from wax-leaf ligustrum grown in shade and in full sun. The thickness in micrometers of the palisade layer was recorded for each type of leaf. Thicknesses of 7 sun leaves were reported as: 150, 100, 210, 300, 200, 210, and 300, respectively. Thicknesses of 7 shade leaves were reported as 120, 125, 160, 130, 200, 170, and 200, respectively. The mean ± standard deviation for sun leaves was 210 ± 73 micrometers and for shade leaves it was158 ± 34 micrometers. Note that since all data were rounded to the nearest micrometer, it is inappropriate to include decimal places in either the mean or standard deviation. For the t test for independent samples you do not have to have the same number of data points in each group. We have to assume that the population follows a normal distribution (small samples have more scatter and follow what is called a t distribution). Corrections can be made for groups that do not show a normal distribution (skewed samples, for example - note that the word 'skew' has a specific statistical meaning, so don't use it as a synonym for 'messed up'). The t test can be performed knowing just the means, standard deviation, and number of data points. Note that the raw data must be used for the t test or any statistical test, for that matter. If you record only means in your notebook, you lose a great deal of information and usually render your work invalid. 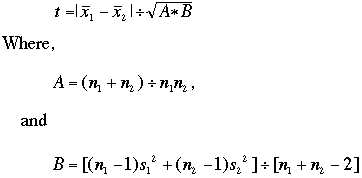The two sample t test yields a statistic t, in which X-bar, of course, is the sample mean, and s is the sample standard deviation. Note that the numerator of the formula is the difference between means. The denominator is a measurement of experimental error in the two groups combined. The wider the difference between means, the more confident you are in the data. The more experimental error you have, the less confident you are in the data. Thus the higher the value of t, the greater the confidence that there is a difference. To understand how a precise probability value can be attached to that confidence you need to study the mathematics behind the t distribution in a formal statistics course. The value t is just an intermediate statistic. Probability tables have been prepared based on the t distribution originally worked out by W.S. Gossett (see below). To use the table provided, find the critical value that corrresponds to the number of degrees of freedom you have (degrees of freedom = number of data points in the two groups combined, minus 2). If t exceeds the tabled value, the means are significantly different at the probability level that is listed. When using tables report the lowest probability value for which t exceeds the critical value. Report as 'p < (probability value).' In the example, the difference between means is 52, A = 14/49, and B = 3242.5. Then t = 1.71 (rounding up). There are (7 + 7 -2) = 12 degrees of freedom, so the critical value for p = 0.05 is 2.18. 1.71 is less than 2.18, so we cannot reject the null hypothesis that the two populations have the same palisade layer thickness. So now what? If the question is very important to you, you might collect more data. With a well designed experiment, sufficient data can overcome the uncertainty contributed by experimental error, and yield a significant difference between samples, if one exists. If you have lots of data and the probability value becomes smaller but still does not reach the 'magic' number 0.05, should you keep collecting data until it does? At this point, consider the biological significance of the question. If you did find adifference of 0.1% between palisade layers of sun and shade leaves respectively, just how important could it be? When reporting results of a statistical analysis, always identify what data sets you compared, what test was used, and for most quantitative data report mean, standard deviation, and the probability values. Make sure the outcome of the analysis is clearly reported. Some spreadsheet programs include the t test for independent variables as a built-in option. Even without a built-in option, is is so easy to set up a spreadsheet to do a paired t test that it may not be worth the expense and effort to buy and learn a dedicated statistics software program, unless more complicated statistics are needed. Historical note You may be wondering where the name 'Student' came from, and why the quotation marks. The basis of the t test would be known as 'Gosset's t distribution' if it werent for contractural obligations that prevented W.S. Gosset from taking credit for its development. Gosset used measurements of the heights and left middle finger lengths of criminals in a local prison to work out the t distribution empirically. The mathematical theory followed. Gosset published his distribution in 1908 under the pseudonym 'Student.'