State III Respiration
State III respiration is defined as ADP-stimulated
respiration. We put isolated mitochondria into
state III when we add ADP to intact, unpoisoned
mitochondria in the presence of excess substrate.
That is, to produce state III we must first produce
state IV. The mechanism for acceleration of respiration
in the presence of ADP was illustrated in the
introduction. ADP binds the enzyme complex ATP synthase.
In the presence of inorganic phosphate, which also
binds ATP synthase, ADP binding opens a channel
that permits the driving of protons into the
matrix from outside the inner membrane. The energy
that is released as protons are driven across
is used to produce ATP. As energy in the
gradient is removed the electron transport
chain spontaneously speeds up. The synthesis
of ATP by mitochondria is called oxidative
phosphorylation.
It must be emphasized that ATP synthase is not
part of the ETS, although it does float around
in the same lipid bilayer as components of the
ETS. It must also be emphasized that the protons
that pass through ATP synthase simply recombine
with hydroxyl ions in the matrix. They are ionization
products of water in this system as they are
in any aqueous system. There is nothing special
about these particular protons. They do not drive
reactions, and they certainly do not reduce oxygen.
Oxygen consumption in state III is caused by
the same process as is oxygen consumption in
state IV. It is catalyzed by cytochrome oxidase
as the last step in electron transport.
In an isolated system, the mitochondria return
to state IV respiration when the ADP is used up.
The state IV rate may be higher than before, due
to an uncoupling effect by ADP itself.
Uncoupling
effect of ADP
Following state III respiration
the state IV rate that resumes
after ADP is used up is often greater than the initial
state IV rate. The observation can be bothersome
when one's research calls for reporting the R.C.R.
(Respiratory Control Ratio, the ratio of state III
to state IV respiration). Having a probable explanation
can be reassuring.
In living cells the ratio of ATP
to ADP is quite high. The concentration of ADP
in a cell never approaches that found in a dissolved
oxygen chamber when an investigator squirts a pile
of it in with a syringe. I'll offer two possible
suggestions for the mechanism by which ADP may
cause an increase in electron transport.
Perhaps there is a nonspecific effect of ADP
on the membrane itself (perhaps the outer, perhaps
the inner, maybe both). That is, in large concentrations
ADP may bind proteins or lipids in the membrane,
creating a channel of sorts or otherwise disrupting
the structure so that protons can move across.
I sort of prefer a more elegant explanation, however.
All living membranes must be maintained constantly
by energy-requiring reactions. In fact, one reason
death occurs so quickly following cyanide poisoning
is that the supply of ATP is completely cut off.
Cells need a constant, immediate supply of ATP.
Without it their membranes begin to deteriorate
immediately. Nerves, in particular, stop conducting
right away, and the victim is history. If the ratio
of ATP to ADP is so unfavorable that 'housekeeping'
reactions are stopped or significantly slowed,
there may be damage to the mitochondrial membranes.
Most likely, some mitochondria become totally uncoupled
while others are able to maintain a gradient.
ADP:Oxygen Ratio
The passage of an electron pair through each of the
proton-translocating complexes (I, III, and IV) is
associated with a drop in free energy that somewhat
exceeds that needed to phosphorylate one molecule
of ADP. The phosphorylation of one mole of ADP requires
30.5 kJ (kilojoules). The free energy released on
the passage of two moles of electrons (they move
in pairs, you know) is 51 kJ through complex I, 41
kJ through complex III, and 100 kJ through complex
IV. Since it is only at these three sites that electron
transport releases enough free energy to phosphorylate
ADP, it was hypothesized that the passage of one
pair of electrons from NADH through the length of
the ETS causes the phosphorylation of three molecules
of ADP (two molecules if the starting point is FADH2).
In the early 1970s, three major hypotheses were
kicking around, to explain the coupling of electron
transport to ADP phosphorylation. The term coupling
refers to how the energy released through electron
transport is transferred to ADP and inorganic phosphate.
One proposal called for a chemical intermediate
to carry energy to an ATP synthetase enzyme, much
like NADH carries energy to the ETS from Krebs
reactions. A second proposal called for a conformational
change in a membrane-bound complex that is directly
associated with each complex. The change in conformation
would store energy, and when ADP and phosphate
bound the complex the energy would be transferred.
The last, the Mitchell hypothesis, was considered
by many to be too far-fetched to be true. The proposal
was that the energy was stored in the form of an
electrochemical gradient, which was then utilized
at a remote site to synthesize ATP.
Support for the first two proposals came in part
from the observation that isolated mitochondria
appear to produce three ATPs per electron pair
via the "long" route, and 2 via the "short" (succinate)
route. However, no one could demonstrate the presence
of the putative chemical intermediate, and no one
could match up binding sites for ADP and phosphate
with any of the complexes of the ETS. It was observed
that the extramitochondrial pH dropped when mitochondria
were in the active state. Under ideal circumstances,
isolated mitochondria could phosporylate slightly
more than three ADPs per oxygen atom.
These and other observations led to universal acceptance
of Peter Mitchell's proposal and his eventual Nobel
Prize.
You can verify that NADH-supported respiration
results in the phosphorylation of 1.5 times as
much ADP as with succinate-supported respiration
by examining the ratio of ADP molecules phosphorylated
to atoms of oxygen consumed (ADP:O ratio).
You will likely observe that the ratios are
not integers and that they are lower with uncoupled
mitochondria and higher with well-coupled mitochondria.
In fact, the ratio can exceed three in very well-coupled
mitochondria (3.3 is about the maximum ratio attainable).
That is because at the 'weakest' point of the chain,
41 kJ of free energy is available, and it only
takes 30.5 kJ to phosphorylate one ADP. The theoretical
maximum ADP:O ratio is not 4 because of the entropy
associated with all processes, and because of utilization
of the chemiosmotic gradient for other processes.
Calculating
an ADP:O Ratio from a Chart Record
One can calculate an ADP:O ratio with minimal knowledge
of the preparation itself. All you need is the total
dissolved oxygen in the chamber from which you measured
oxygen consumption, the total amount of ADP added
to the chamber, and the percent of total oxygen
that was used up in order to phosphorylate all of
the ADP. Total oxygen is obtained by multiplying
chamber volume by the known volume of dissolved
oxygen per unit volume at the temperature of the
experiment (0.237 micromoles molecular oxygen per
ml at room temperature for a typical respiration
medium).
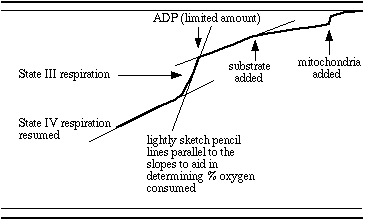
Determine the amount of ADP added in µmoles
or nmoles. Determine total oxygen in the chamber
by multiplying chamber volume by the solubility
factor in µmoles (or nmoles). Using a straightedge,
define the slopes with light pencil lines and determine
where the slopes intersect. Measure the percent
of record (percent total oxygen) used during state
III respiration by determining the distance between
intersections at the start and end of state III.
Convert to a fraction and multiply the fraction
by total oxygen to get the amount of molecular
oxygen used. Multiply by 2 to get the amount of
atomic oxygen
used. Divide the amount of ADP added by the amount
of atomic oxygen consumed.
Example
Let the chamber volume be 2 ml and solubility
factor 0.237 micromoles/ml. Suppose the addition
of 20 µl 0.01M ADP resulted in a 10% drop
in total oxygen during state III respiration. Then
200 nmoles (0.2 µmoles) ADP was added to
a chamber containing a total, at the beginning
of the experiment, of 2 x 237 = 474 nmoles (0.474 µmoles)
molecular oxygen. Molecular oxygen consumed was
0.10 x 474 = 47.4 nmoles (0.0474µmoles),
which is 94.8 nmoles (0.0948 µmoles) atomic
oxygen. The ADP:O ratio is given by 200 divided
by 94.8, which is 2.1. Note that the ratio is reported
to two significant figures, which is reasonable
given the uncertainty of measuring volumes and
the points at which the slope changed.
Report a realistic and
appropriate ADP:O ratio
Students often report ADP:O ratios that are unrealistically
precise. A ratio of 2.9885462, for
example, suggests an impossible level of precision.
Consider how accurately you can measure the slope
of an oxygraph record before reporting ratios to
several decimal places.
Some students report ADP:O ratios
for every experiment in which ADP was added to the chamber, even
when state III respiration was not produced. If
there is no state III, then there is no ATP synthesis
and there cannot be an ADP:O ratio.
Students often report unrealistic values for ADP:O
ratios. The quality of a preparation affects the
ratio, but not so much that the ratio can be off
by an order of magnitude. Even our best preparations
will not produce ratios much above 3. Typical ratios
for succinate and glutamate supported respiration
approach 2 and 3, respectively.
Factors other than the condition of mitochondria
affect ADP:O ratios. The amount of ADP added to
a chamber determines how much oxygen will be consumed
during the state III rate. In addition to the accuracy
with which the ADP is drawn up and delivered, the
concentration of the solution itself may be low
or high. ADP deteriorates with time, so that a
stored solution will be at lower concentration
that when it was originally made up. On the other
hand, a common student error is to thaw a stock
solution and use it immediately without re-mixing
the materials. As an aqueous solution freezes,
the most dilute part freezes first. Since
ice floats, the most concentrated part is at the
bottom of the sample tube, and students usually
go to the bottom when drawing liquid from a tube.
It is critical to mix previously frozen stock
solutions and samples before using them, usually
by inverting and agitating the completely thawed
solution repeatedly.
You may discover that upon the addition of an
inhibitor of electron transport such as cyanide,
that the chamber actually gains oxygen.
Of course, there is no biochemical mechanism by
which mitochondria evolve oxygen. The gain is from
oxygen diffusing back into the chamber through
a leaky seal or through the sample port. If such
diffusion can occur at the end of the experiment,
it certainly could take place (and was taking
place) during the experiment itself.
Notice that some of the factors affecting ADP:O
ratios tend to increase the measured ratios while
others tend to decrease them. A discussion in a
research paper should focus on the results themselves.
Suppose one obtains an ADP:O ratio that is unusually
low. A superficial discussion lists all of the
factors that can affect ADP:O ratios without regard
to which factors lower the measured ratio and which
raise it. The reader will be interested in likely
reasons for the observed result, not in every possible
explanation for every possible observation.
Is entropy necessarily a bad thing?
In living cells mitochondria are never idle. They
exercise respiratory control, with electron
transport slowing or increasing as the energy in
the chemiosmotic gradient is decreasingly or increasingly
utilized. Much of the energy released during Krebs
reactions and electron transport is converted to
random molecular motion (heat). In fact, any reaction
results in an increase in entropy of the universe
(second law of thermodynamics). Should we despair
this waste of valuable free energy?
We homeotherms maintain
a constant internal temperature within physiological
limits. Regulating body temperature requires
regulating both heat production and heat loss.
Mitochondria metabolism is an important source
of heat production. For the most part, variations
in the rate of electron transport are directly
related to the demand by the cells for ATP. To
some extent the rate also depends on the need to
maintain a basal metabolic rate (BMR). We even
have mechanisms for varying the extent to which
mitochondria are uncoupled, so as to increase or
decrease heat production on a long term basis.
|
