Using a Counting Chamber

For microbiology, cell culture, and many applications that require use of suspensions of cells it is necessary to determine cell concentration. One can often determine cell density of a suspension spectrophotometrically, however that form of determination does not allow an assessment of cell viability, nor can one distinguish cell types.

A device used for determining the number of cells per unit volume of a suspension is called a counting chamber. The most widely used type of chamber is called a hemocytometer, since it was originally designed for performing blood cell counts.

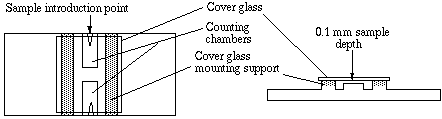
To prepare the counting chamber the mirror-like polished surface is carefully cleaned with lens paper. The coverslip is also cleaned. Coverslips for counting chambers are specially made and are thicker than those for conventional microscopy, since they must be heavy enough to overcome the surface tension of a drop of liquid. The coverslip is placed over the counting surface prior to putting on the cell suspension. The suspension is introduced into one of the V-shaped wells with a pasteur or other type of pipet. The area under the coverslip fills by capillary action. Enough liquid should be introduced so that the mirrored surface is just covered. The charged counting chamber is then placed on the microscope stage and the counting grid is brought into focus at low power.

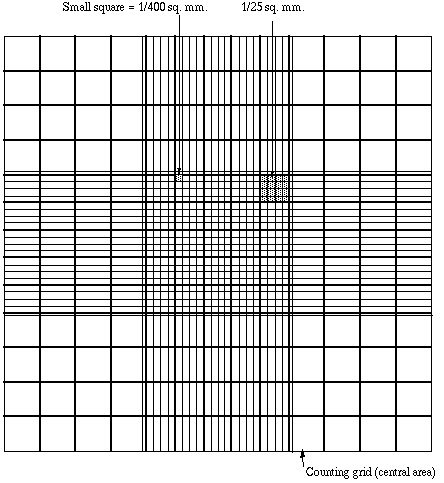
It is essential to be extremely careful with higher power objectives, since the counting chamber is much thicker than a conventional slide. The chamber or an objective lens may be damaged if the user is not not careful. One entire grid on standard hemacytometers with Neubauer rulings can be seen at 40x (4x objective). The main divisions separate the grid into 9 large squares (like a tic-tac-toe grid). Each square has a surface area of one square mm, and the depth of the chamber is 0.1 mm. Thus the entire counting grid lies under a volume of 0.9 mm-cubed.

Suspensions should be dilute enough so that the cells or other particles do not overlap each other on the grid, and should be uniformly distributed. To perform the count, determine the magnification needed to recognize the desired cell type. Now systematically count the cells in selected squares so that the total count is 100 cells or so (number of cells needed for a statistically significant count). For large cells this may mean counting the four large corner squares and the middle one. For a dense suspension of small cells you may wish to count the cells in the four 1/25 sq. mm corners plus the middle square in the central square. Always decide on a specific counting patter to avoid bias. For cells that overlap a ruling, count a cell as "in" if it overlaps the top or right ruling, and "out" if it overlaps the bottom or left ruling.

Here is a way to determine a particle count using a Neubauer hemocytometer. Suppose that you conduct a count as described above, and count 187 particles in the five small squares described. Each square has an area of 1/25 mm-squared (that is, 0.04 mm-squared) and depth of 0.1 mm. The total volume in each square is (0.04)x(0.1) = 0.004 mm-cubed. You have five squares with combined volume of 5x(0.004) = 0.02 mm-cubed. Thus you counted 187 particles in a volume of 0.02 mm-cubed, giving you 187/(0.02) = 9350 particles per mm-cubed. There are 1000 cubic millimeters in one cubic centimeter (same as a milliliter), so your particle count is 9,350,000 per ml.

Cells are often large enough to require counting over a larger surface area. For example, you might count the total number of cells in the four large corner squares plus the middle combined. Each square has surface area of 1 mm-squared and a depth of 0.1 mm, giving it a volume of 0.1 mm-cubed. Suppose that you counted 125 cells (total) in the five squares. You then have 125 cells per 0.5 mm-cubed, which is 250 cells/mm-cubed. Again, multiply by 1000 to determine cell count per ml (250,000).

Sometimes you will need to dilute a cell suspension to get the cell density low enough for counting. In that case you will need to multiply your final count by the dilution factor. For example, suppose that for counting you had to dilute a suspension of Chlamydomonas 10 fold. Suppose you obtained a final count of 250,000 cells/ml as described above. Then the count in the original (undiluted) suspension is 10 x 250,000 which is 2,500,000 cells/ml.