Chapter 5 - Conservation of Charge

 

OVERVIEW

 

Conservation of charge is the focus of Chapter 5.� The challenge problem is neuroprosthetic devices;� worked example problems include a transistor sensor that converts a chemical signal to an electrical signal and modeling a neuron.� Kirchhoff�s Current Law is the reduction of the conservation of rate of charge for a steady-state system.� Classical examples in circuit analysis are used to illustrate Kirchhoff�s Current Law.� Radioactive decay, acid and base dissociation, and electrochemical reactions illustrate reacting systems.� The charging of a capacitor is given as an example of a dynamic system.� The electrical energy accounting statement is then developed.� The concept of resistance and Kirchhoff�s Voltage Law are illustrated in several circuit examples.� Analogous sections to those described above delineate examples of reacting systems and dynamic systems such as those including inductors.�

 

 

EXAMPLE PROBLEMS

 

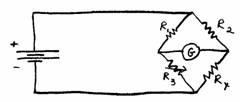
1.� The figure shows a schematic of a Wheatstone bridge, a circuit configuration used to measure unknown resistances.� For example, in bioengineering the Wheatstone bridge is often used in gages that evaluate mechanical properties of bones, muscles, and cells because the resistances of those materials change with mechanical deformation.� The circuit element denoted G represents a galvanometer, a device that measures small amounts of current.� Resistances R₁ and R₂ are fixed and known.� To determine the resistance R_x, R₃ is varied so that the current through the galvanometer is zero.� Using Ohm�s law with Kirchhoff�s current and voltage laws, determine the unknown resistance (R_x) in terms of the known resistances.� (Nilsson JW, Riedel SA.� Electric Circuits:� Sixth Edition, p. 77-78)

 

 

2.� Einthoven�s Triangle:� During an ECG, the potential of three limbs is taken relative to the average electric potential of the body.� The right arm has a potential of �0.15 mV, the left arm has a potential of +0.55 mV, and the potential of the left leg is +0.93 mV.� What is the magnitude and angle of deflection of the cardiac vector?

 

3.� Iodine-131, a radioactive isotope of iodine, is used to test thyroid function and treat thyroid disorders, such as hyperthyroidism or cancer.�

 

A.)  The decay of ¹³¹I results in release of a beta particle and gamma radiation as well as a stable element.� What is this stable element? Write out the decay reaction of ¹³¹I.

 

B.)  Given that the half-life of ¹³¹I is approximately 8 days, how much negative charge does 25 g of iodine lose as beta particles in 15 days as it decays? (A decay reaction may be modeled by the equation:

 

 

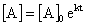
where k is the rate constant, t is time, [A] is the quantity of interest of substance A, [A]₀ is the initial quantity of substance A.)

 

 

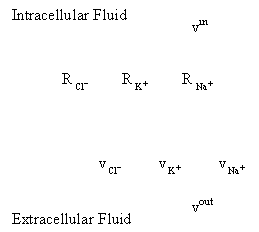
4.� A electrical capacitor consists of two conductors separated by an insulator.� By this definition, the cell membrane can be modeled as a capacitor, with the intracellular fluid and extracellular fluid being the two conductors and the membrane as the insulating layer.� The cell membrane is more complicated than a simple capacitor, however, because there are ion channels which allow ion flow, and thus current.� Thus, the cell membrane is modeled as[1]:

 

����������������������� Fig. 5.**

 

�

 

 

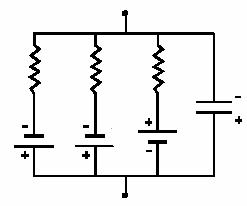
The resistors represent the resistance through the ion channels to ion flow.� The voltage sources (batteries) represent the potential difference across the membrane caused by concentration gradients of each type of ion.

 

����������� Given this model of the cell membrane, derive an equation for the current across of the cell membrane, i_m, in terms of the capacitance, potential differences and resistances of the ions in the model, and the overall potential difference across the membrane.