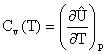Chapter 4 - Conservation of
Energy
OVERVIEW
Conservation of energy is the topic of Chapter 4. The challenge problem explores different
types of energy and how they may be harnessed, including renewable biomass
resources; worked example problems
include enthalpy change during photosynthesis, hydroelectric power, and
photosynthesis in green plants.
Potential, kinetic and internal energy and enthalpy and their rates are
defined and illustrated. The movement of
energy as heat and work is discussed.
Energy balances are illustrated first for closed and isolated systems
through classic thermodynamic examples such as the expansion of a gas. Significant attention is spent developing
calculation strategies for changes in enthalpy due to changes in temperature,
pressure and phase. With these tools,
open, steady-state systems such as heat loss during breathing are
illustrated. Enthalpy changes associated
with chemical reactions are calculated using heats of formation or
combustion. Complete and incomplete respiration
in the human body are given as examples.
Dynamic systems include the start-up of a bioreactor and the use of
basal metabolic rate to estimate weight gain.
EXAMPLE PROBLEMS
- The
heat capacity at constant pressure, Cp, is the slope of the
change in specific enthalpy as a function of temperature, as
given in equation [6.4-4]:
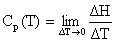
The limit as T 0 becomes
0 becomes
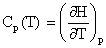
where the 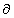 indicates a partial derivative. Partial derivatives are used when a function
(
indicates a partial derivative. Partial derivatives are used when a function
(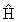 in this case) is dependent on more than one variable (T and
P in this case). For the purposes of
this problem, the partial derivative can be treated like an ordinary
derivative.
in this case) is dependent on more than one variable (T and
P in this case). For the purposes of
this problem, the partial derivative can be treated like an ordinary
derivative.
There is a similar relationship
between the heat capacity at constant volume, Cv, and the partial
derivative of specific internal energy, U, with respect to temperature, as
follows:
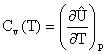
From these heat capacity
definitions and the definition of enthalpy given in this chapter, derive the
relationship between Cp and Cv for an ideal gas in terms
of n (the number of moles), R (ideal gas constant), and other variables that
may be necessary.
- You
are to size a continuous vaporizer for a child's sick room. The device
receives liquid water at 20°C and 1 atm and produce
steam at a rate of 0.7 g/min. At what rate must energy be supplied if the
device is 100% efficient? The standard heat of vaporization of water is
2256.9 kJ/kg and specific heat capacity of water is 1cal/°C-g.
- Adenosine
triphosphate (ATP) is a major source of energy for cells in the body. Energy is released when one of the
phosphate bonds is broken to form adenosine diphosphate (ADP).

Given the following
thermodynamic data, find the heat of reaction for the forward reaction.
|
Species
|
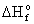 (kJ/mol) (kJ/mol)
|
|
Adenosine
triphosphate (ATP)
|
-2981.79
|
|
H2O
|
-286.65
|
|
Adenosine
diphosphate (ADP)
|
-2000.19
|
|
Pi
|
-1299.13
|
- A biotechnology firm has just
constructed a new genetically engineered Escherichia coli
strain that is capable of producing an important recombinant protein. It
was found that the production of this recombinant protein is proportional
cell growth. Ammonia is used as nitrogen source for aerobic respiration of
glucose. The recombinant protein has an overall formula CH1.55O1.31N0.25.
The yield of biomass from glucose is determined to be 0.48 g g-1 (g
of biomass formed per g of glucose consumed); the yield of recombinant
protein from glucose is about 20% that for cells. The following equation can be used to
represent the production process:
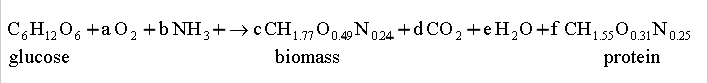
where a, b, c, d, e and f are the
stoichiometric coefficients.
Suppose a continuous bioreactor with a
working volume of 100 liter is used to produce the recombinant protein. A
stream of medium containing essential nutrient including glucose and ammonia
flows into the reactor at a rate of 10 l/hr. The medium contains 50 g/L of
glucose and sufficient quantity of ammonia (as calculated later). The exit stream
contains the cells that harbor the recombinant protein. Under these conditions,
only negligible quantity of glucose can be detected in the exit stream (that
is, all glucose can be assumed to be consumed in the reactor). The temperature
of the inlet stream and the bioreactor are set at 25°C. Assume the
reactor is well insulated and the amount of shaft work involved due to mixing
is negligible.
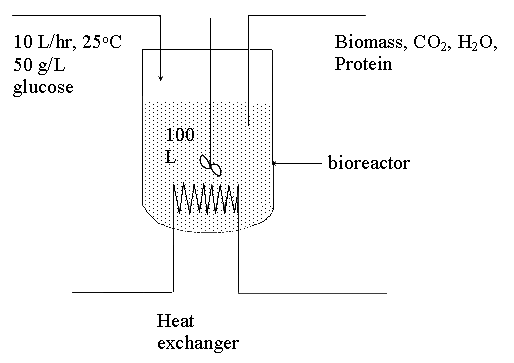
Suppose the reactor has been operated for a
while and is at steady state, do the following:
A.) How much ammonia is required?
B.) What is the recombinant protein production rate?
C.) It is proposed that the heat of reaction
can be related to the oxygen consumption rate by the following expression:
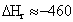 kJ/mol of oxygen consumed
kJ/mol of oxygen consumed
How good
is this correlation when compared with that calculated from using the heat of
combustion?
D.) What is the heat addition/removal rate in order to maintain the
reactor at 25°C?
E.) In the middle of the run, the heat
exchanger malfunctioned; as a result, no heat can be added or removed from the
reactor. Assume that culture behavior remains the same as before within this
temperature range (this may not be a good assumption). What is the temperature
of the reactor one hour after the mishap? Assume there is no heat loss from the
reactor to the surrounding.
Data:
· Standard
heat of combustion of glucose, 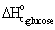 = -2,805 kJ/mol
= -2,805 kJ/mol
· Standard
heat of combustion of ammonia, 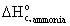 = -382.6 kJ/mol
= -382.6 kJ/mol
· Standard
heat of combustion of biomass, 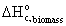 = -551 kJ/mol
= -551 kJ/mol
· Standard
heat of combustion of recombinant protein, 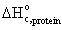 = -567 kJ/mol
= -567 kJ/mol
· Assume the specific heat
capacity of medium and broth are similar to that of water = 1 cal/g
· Assume the density of medium
and broth are similar to that of water = 1 g/cm3
Hints:
- Since the yield of biomass from glucose is
determined to be 0.48 g g-1 (g of biomass formed per g of
glucose consumed), this implies that c = 3.46 mol mol-1;
·
Since the yield of recombinant protein from
glucose is about 20% that for cells, that implies the yield is (0.2)(0.48) =
0.096 g g-1 (g of recombinant protein produced per g of glucose
consumed).