Projects
Although implementations of these model systems encompass a wide variety of experimental and theoretical techniques from across the CM and AMO disciplines, there are certain common pieces of physics that tie these projects together and form a starting point for common discussions between Fellows, Scholars, and faculty:The Hubbard model in optical lattices
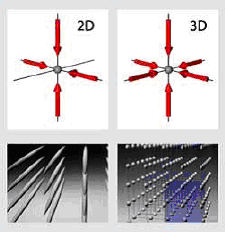 In strongly interacting problems, the standard approach of condensed matter physics - to assume that interactions between particles are weak, and therefore all one needs to do to understand the states of many particles is to consider each particle one at a time - is a poor strategy. One archetype of such a strongly interacting problem is the so-called two-dimensional Hubbard model. This is a model that was originally suggested to contain much of the essential physics behind high temperature superconductivity. In this model, fermion particles (electrons in real solids; atoms in the atomic physics analog described below) are placed in a square, two-dimensional grid of sites. For each particle considered one at a time, there is some quantum mechanical amplitude for tunneling to the adjacent site. However, the interactions between particles are not weak - indeed, the interactions are so strong and repulsive that each site can never be occupied by more than a single particle. Each particle possesses a spin degree of freedom that can be thought of as like a little bar magnet. For the case of one particle per site, the lowest energy state of this system is thought to be an insulator (the particles are essentially locked in place because of their strong interactions), and is thought to be an antiferromagnet (spins on neighboring sites point in opposite directions).
An enormous amount of theory has been dedicated to understanding the excitations of this system, and how this system evolves as the population of particles is changed away from the one-per-site ratio. Detailed examinations in real solids (such as high temperature superconductors, where the sites correspond to the copper atoms in a copper oxide plane) are extremely difficult, since changing the electronic population usually involves changing the chemistry of the material. However, recent advances in working with trapped cold atoms in optical lattices mean that it is now possible to set up an implementation of the 2d Hubbard model, with trapped fermionic atoms playing the role of the electrons. Randy Hulet is preparing to examine just such a system, and the tunability afforded by the optical trap techniques will allow unprecedented examination of the different phases possible in the 2d Hubbard model. This is exactly the sort of project suited to the effort outlined above: atomic physics methods can be used to implement a tunable idealization of a tremendously interesting and important strongly interacting quantum magnetism materials problem.
In strongly interacting problems, the standard approach of condensed matter physics - to assume that interactions between particles are weak, and therefore all one needs to do to understand the states of many particles is to consider each particle one at a time - is a poor strategy. One archetype of such a strongly interacting problem is the so-called two-dimensional Hubbard model. This is a model that was originally suggested to contain much of the essential physics behind high temperature superconductivity. In this model, fermion particles (electrons in real solids; atoms in the atomic physics analog described below) are placed in a square, two-dimensional grid of sites. For each particle considered one at a time, there is some quantum mechanical amplitude for tunneling to the adjacent site. However, the interactions between particles are not weak - indeed, the interactions are so strong and repulsive that each site can never be occupied by more than a single particle. Each particle possesses a spin degree of freedom that can be thought of as like a little bar magnet. For the case of one particle per site, the lowest energy state of this system is thought to be an insulator (the particles are essentially locked in place because of their strong interactions), and is thought to be an antiferromagnet (spins on neighboring sites point in opposite directions).
An enormous amount of theory has been dedicated to understanding the excitations of this system, and how this system evolves as the population of particles is changed away from the one-per-site ratio. Detailed examinations in real solids (such as high temperature superconductors, where the sites correspond to the copper atoms in a copper oxide plane) are extremely difficult, since changing the electronic population usually involves changing the chemistry of the material. However, recent advances in working with trapped cold atoms in optical lattices mean that it is now possible to set up an implementation of the 2d Hubbard model, with trapped fermionic atoms playing the role of the electrons. Randy Hulet is preparing to examine just such a system, and the tunability afforded by the optical trap techniques will allow unprecedented examination of the different phases possible in the 2d Hubbard model. This is exactly the sort of project suited to the effort outlined above: atomic physics methods can be used to implement a tunable idealization of a tremendously interesting and important strongly interacting quantum magnetism materials problem.
Nanostructures to probe quantum criticality
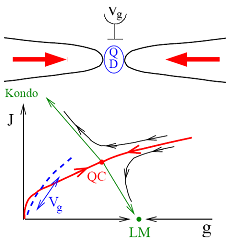 In classical phase transitions, like the boiling of liquids, fluctuations around the transition are thermally driven. In strongly interacting quantum systems, it is possible for fluctuations near phase transitions to be driven by quantum "zero point" motion. One class of materials that shows quantum phase transitions and so-called quantum criticality is the heavy fermion compounds. In these materials, there is a competition between conduction electrons interacting with individual magnetic moments of rare earth metal atoms, and electrons interacting with collective "spin wave" excitations of all the magnetic moments. As the relative strength of the couplings is tuned (again, usually through either chemistry or pressure), the system can undergo a quantum phase transition between a "normal" metallic state, and an unusual metallic state. As in the Hubbard model above, detailed microscopic understanding of these states in bulk materials has been very challenging.
Qimiao Si and collaborators have argued that new nanostructures, specifically single-molecule transistors with ferromagnetic leads, can be used as a model system to examine just this kind of quantum phase transition. Doug Natelson is preparing to fabricate and examine such devices. Again, this is a case where a model system (this time one based on a nanostructure) can be used to examine a strongly interacting, quantum magnetism / quantum materials problem with unprecedented tunability. Further analysis and experiments may bring to light ways of more closely modeling such systems with atomic physics techniques as well.
In classical phase transitions, like the boiling of liquids, fluctuations around the transition are thermally driven. In strongly interacting quantum systems, it is possible for fluctuations near phase transitions to be driven by quantum "zero point" motion. One class of materials that shows quantum phase transitions and so-called quantum criticality is the heavy fermion compounds. In these materials, there is a competition between conduction electrons interacting with individual magnetic moments of rare earth metal atoms, and electrons interacting with collective "spin wave" excitations of all the magnetic moments. As the relative strength of the couplings is tuned (again, usually through either chemistry or pressure), the system can undergo a quantum phase transition between a "normal" metallic state, and an unusual metallic state. As in the Hubbard model above, detailed microscopic understanding of these states in bulk materials has been very challenging.
Qimiao Si and collaborators have argued that new nanostructures, specifically single-molecule transistors with ferromagnetic leads, can be used as a model system to examine just this kind of quantum phase transition. Doug Natelson is preparing to fabricate and examine such devices. Again, this is a case where a model system (this time one based on a nanostructure) can be used to examine a strongly interacting, quantum magnetism / quantum materials problem with unprecedented tunability. Further analysis and experiments may bring to light ways of more closely modeling such systems with atomic physics techniques as well.
Optical lattices: Quantum magnetism and phase transitions in dipolar gases
 Beyond the Hubbard model, low-energy effective models with spin-dependent interactions underlie our understanding of many condensed matter phenomena, including the magnetic properties of insulators. Bose-condensed atoms and molecules with electric or magnetic dipole moments in optical lattices may also be used as ideal realizations of these models and provide control over interaction strengths and excellent diagnostics of the state of the system. Recent theoretical work has highlighted that long-range dipole-dipole interactions in such systems, through their interplay with the short-range exchange interactions, can lead to ferromagnetism, spin wave collective excitations, and a rich quantum phase structure involving insulators, superfluids, and supersolids.
There are two extreme models for magnetism in solids. The Bloch picture is based on exchange interactions in a free electron gas and is believed to provide a qualitatively correct explanation for ferromagnetism in metals where electrons are itinerant. In the Heisenberg picture, the electron spins are well localized. Hence the Heisenberg model is more suitable for insulating or dielectric systems. In ultracold gases of atoms or molecules confined in an optical lattice, by varying the strength of the lattice potential, and hence the tunneling rate between neighboring sites, it should be possible to tune continuously between Bloch and Heisenberg limits, thus addressing issues in the theory of magnetism that have never been satisfactorily resolved.
Furthermore, most bulk solid magnetic materials are dominated by strong exchange interactions. For spins with rotational symmetry and in two spatial dimensions, it is well known that long-range order does not occur at any finite temperature if only the exchange interaction is present. In ultracold gases, the Fermi contact interaction acts as an effective exchange interaction. The strength of the contact interaction is related to the tunneling rate and hence can be tuned in the same fashion as discussed above. Therefore the relative strengths of the contact exchange interaction and the long-range interactions (e.g., the dipole-dipole or quadrupole-quadrupole interactions) can be easily varied, facilitating a detailed study of quantum phase transitions between different magnetically ordered states.
Beyond the Hubbard model, low-energy effective models with spin-dependent interactions underlie our understanding of many condensed matter phenomena, including the magnetic properties of insulators. Bose-condensed atoms and molecules with electric or magnetic dipole moments in optical lattices may also be used as ideal realizations of these models and provide control over interaction strengths and excellent diagnostics of the state of the system. Recent theoretical work has highlighted that long-range dipole-dipole interactions in such systems, through their interplay with the short-range exchange interactions, can lead to ferromagnetism, spin wave collective excitations, and a rich quantum phase structure involving insulators, superfluids, and supersolids.
There are two extreme models for magnetism in solids. The Bloch picture is based on exchange interactions in a free electron gas and is believed to provide a qualitatively correct explanation for ferromagnetism in metals where electrons are itinerant. In the Heisenberg picture, the electron spins are well localized. Hence the Heisenberg model is more suitable for insulating or dielectric systems. In ultracold gases of atoms or molecules confined in an optical lattice, by varying the strength of the lattice potential, and hence the tunneling rate between neighboring sites, it should be possible to tune continuously between Bloch and Heisenberg limits, thus addressing issues in the theory of magnetism that have never been satisfactorily resolved.
Furthermore, most bulk solid magnetic materials are dominated by strong exchange interactions. For spins with rotational symmetry and in two spatial dimensions, it is well known that long-range order does not occur at any finite temperature if only the exchange interaction is present. In ultracold gases, the Fermi contact interaction acts as an effective exchange interaction. The strength of the contact interaction is related to the tunneling rate and hence can be tuned in the same fashion as discussed above. Therefore the relative strengths of the contact exchange interaction and the long-range interactions (e.g., the dipole-dipole or quadrupole-quadrupole interactions) can be easily varied, facilitating a detailed study of quantum phase transitions between different magnetically ordered states.
Nanostructures to examine spin-charge separation and dynamic scaling in 1d
 Single-walled carbon nanotubes (SWNTs) are an example of a nanostructured system with a truly one-dimensional band structure. In such 1d systems, the standard (Fermi liquid) description of electronic conduction in metals breaks down9; rather, the ground state of the system is expected to be a Tomonaga-Luttinger liquid (TLL). Unlike the situation in ordinary metals, the low energy excitations of a TLL are collective in character, with spin and charge excitations propagating at different speeds. This spin-charge separation is among the most exotic features of the TLL and is relevant to other strongly correlated systems, perhaps including the high temperature superconductors. SWNTs are ideal model systems for examining this physics because they are expected to have very long spin relaxation lengths due to their long elastic mean free paths and weak spin-orbit coupling. Electron spin resonance (ESR) is expected to be a powerful probe of spin-charge separation physics, via lineshapes and the evolution of ESR frequencies with temperature and magnetic field.
Another interesting and relevant question is whether the optical conductivity in metallic SWNTs satisfies omega/T scaling. This would imply that the inelastic relaxation rate for charge carriers is linear in T, a condition that can only occur in metals at a quantum critical point between two quantum phases. A Tomonaga-Luttinger liquid (TLL) has the characteristic feature that it is quantum critical over a finite range of parameters due to enhanced quantum fluctuations in 1D. THz optical measurements as a function of temperature will allow the characterization of the optical conductivity over a broad portion of parameter space.
Single-walled carbon nanotubes (SWNTs) are an example of a nanostructured system with a truly one-dimensional band structure. In such 1d systems, the standard (Fermi liquid) description of electronic conduction in metals breaks down9; rather, the ground state of the system is expected to be a Tomonaga-Luttinger liquid (TLL). Unlike the situation in ordinary metals, the low energy excitations of a TLL are collective in character, with spin and charge excitations propagating at different speeds. This spin-charge separation is among the most exotic features of the TLL and is relevant to other strongly correlated systems, perhaps including the high temperature superconductors. SWNTs are ideal model systems for examining this physics because they are expected to have very long spin relaxation lengths due to their long elastic mean free paths and weak spin-orbit coupling. Electron spin resonance (ESR) is expected to be a powerful probe of spin-charge separation physics, via lineshapes and the evolution of ESR frequencies with temperature and magnetic field.
Another interesting and relevant question is whether the optical conductivity in metallic SWNTs satisfies omega/T scaling. This would imply that the inelastic relaxation rate for charge carriers is linear in T, a condition that can only occur in metals at a quantum critical point between two quantum phases. A Tomonaga-Luttinger liquid (TLL) has the characteristic feature that it is quantum critical over a finite range of parameters due to enhanced quantum fluctuations in 1D. THz optical measurements as a function of temperature will allow the characterization of the optical conductivity over a broad portion of parameter space.
Nanostructures: Quantum Hall edge states
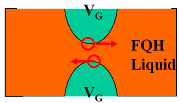 A high-mobility 2d electron system hosted in an ultra-pure GaAs/AlGaAs quantum structure is a clean laboratory for correlation physics. While the fractional quantum Hall effect (FQH) is probably best known and well studied, a multitude of novel quantum phases have been discovered. The deep conceptual connection between CM and AMO physics in the context of fractional quantum Hall effect is exemplified by the proposal to observe FQH state in a rotating cold atomic gas, instead of 2d electrons in an intense magnetic field. Low energy excitations of FQH systems can exhibit unusual fractional quantum numbers, purely as a result of electronic correlations. Prof. Du has a strong interest in searching for signatures of even more exotic physics: quasiparticles that obey non-Abelian statistics.
A high-mobility 2d electron system hosted in an ultra-pure GaAs/AlGaAs quantum structure is a clean laboratory for correlation physics. While the fractional quantum Hall effect (FQH) is probably best known and well studied, a multitude of novel quantum phases have been discovered. The deep conceptual connection between CM and AMO physics in the context of fractional quantum Hall effect is exemplified by the proposal to observe FQH state in a rotating cold atomic gas, instead of 2d electrons in an intense magnetic field. Low energy excitations of FQH systems can exhibit unusual fractional quantum numbers, purely as a result of electronic correlations. Prof. Du has a strong interest in searching for signatures of even more exotic physics: quasiparticles that obey non-Abelian statistics.
Theoretical connections
The experiments described above are unified by common theoretical concepts and approaches. Spin-charge separation is one such concept that links together multiple experimental areas as discussed above. Spin-charge separation is, in that context, a low-energy long-wavelength effective description that provides the simplest and most concise picture of the physics of strongly interacting 1d systems, whether they be trapped ultracold gases or electrons in carbon nanotubes. Such language is unfortunately not readily available in the 2d case. However, the Kondo model relevant to the SMT investigations of quantum criticality is the only known model Hamiltonian written in terms of electrons and for which spin-charge separation is exact at all energies. More generally, the work on cold atom structures and the SMT, nanotube, and QH edge structures is all integrated into the broad effort to understand correlation-induced quantum phases and quantum criticality. Along a similar line, non-equilibrium and finite frequency aspects of the physical properties in the theoretical models will be pursued. For the quantum criticality of the magnetic SMT structure, for instance, the existing theoretical work on the linear-response conductance will be extended to the even more experimentally relevant case of the non-equilibrium setting produced by a finite bias voltage, through a Keldysh approach; this work has the potential to serve as a prototype study of non-equilibrium properties of quantum criticality in general. The finite frequency properties of a Luttinger liquid will be pursued in connection with the dynamical measurements in the SWNTs. Finally, non-equilibrium studies will also be naturally important for the cold-atom experiments.
