An Illustrated Discussion of the Membrane Potential Concept

Take any living cell, and once some technical difficulties are overcome one can measure a potential difference across the cell membrane. The membrane potential is critical for maintenance of the integrity of the cell membrane including the protein complexes within the lipid bilayer, and for signal transduction in excitable cells such as nerve and muscle. To understand how nerves conduct information or how muscles are induced to contract, one must first understand the origin of the membrane potential.

The concepts presented here are really not difficult, but because they are new to most of us, it helps to "see" them, not just read about them. After all, the most successful theoretical scientists think in pictures, not mathematical equations. Although there is a lot of text in this manuscript (probably too much), the pictures should tell the real story.

As with any unfamiliar concept, it is helpful to start with a simple situation and work up to the more complex, real situation. We'll start this discussion with the concept of an equilibrium potential.

Equilibrium potential concept

The first model to explain the origin of the membrane potential of cells was in fact an equilibrium potential model. It is essential to fully understand the concept of an equilibrium potential in order to understand the refinements that were added to develop the current model.

Concentration cells

Picture two compartments of fixed volume, separated by a thin membrane that allows water to move in either direction but is selectively permeable to solutes. Select a membrane that is permeable to potassium ions but impermeable to an anion we will call A-.

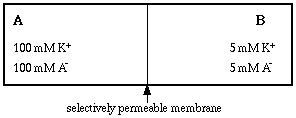
Now simultaneously fill each compartment with potassium salt, so that compartment A contains 100 mM KA and compartment B contains 5 mM KA. Note that at time zero there is complete electrical neutrality in each compartment, that is, there is an equal number of cations and anions.

This establishes a concentration gradient for KA such that the solute tends to diffuse from compartment A to compartment B (why?). The solute KA has dissociated into K+ and A-, and A- can't diffuse across the membrane, so only K+ moves.

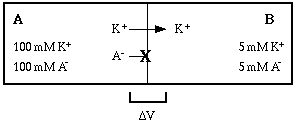
Now if there was no such thing as electrostatic force, potassium ions would continue to diffuse across the membrane until the concentration was equal on both sides. However, each potassium ion that crosses carries a positive charge with it. Thus a potential difference develops across the membrane. The potential difference opposes the movement of potassium ion.

The special properties of a semipermeable membrane can allow it to separate ion pairs, creating an asymmetric distribution of charge across it. There is no excess of either positive or negative charge in the system itself.

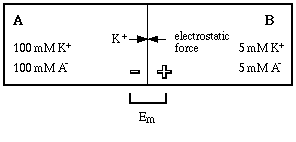
At equilibrium the force of the chemical gradient is offset by the opposing electrostatic force (Em) so that no more potassium ion can move into compartment B. At that point the potential difference across the membrane is called the equilibrium potential for potassium (EK+). The equilibrium potential is a consequence of the displacement of positive ions across the membrane.

Principle #1: A membrane potential is the direct result of an asymmetric distribution of charge (ions) across the membrane.

Notice that in all of the illustrations the concentrations of K+ and A- are the same. This was not an oversight. The actual number of ions that shifted out of compartment A was very small compared to the total number of ions in the compartment. In fact, there was no significant change in ion concentration in either compartment (why?).

Principle #2: The number of displaced ions during development of an equilibrium potential is vanishingly small, so that no change in ion concentration can be detected in any compartment as a result of ionic diffusion.

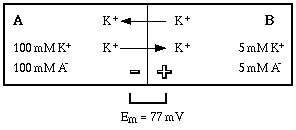
Once the equilibrium is established, potassium ions continue to move back and forth across the membrane. Now, however, the probability that an ion will cross from A to B equals the probability that it will cross from B to A, so there is no net flow of ion in either direction.

Principle #3: In an equilibrium situation diffusion continues at an equal rate in both directions, so there is no net flow of ion in either direction.

The equilibrium potential that develops can be calculated using the Nernst equation for potassium. In the example the potential difference would be 77 mV.

Changes to an equilibrium potential

Now let's see what happens when the concentration of KA is changed in one of the compartments. We'll suddenly dump more KA into compartment B, and assume that it instantaneously dissolves completely, so that the concentration is instantaneously brought to 50 mM.

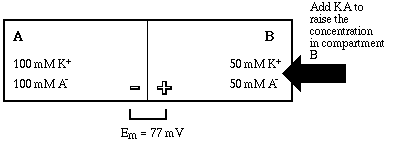
Raising the concentration of the salt in compartment B has no effect on the electrical neutrality of the entire system. That is, before and after the addition the sum of positive and negative charges in A + B is zero. Prior the the addition of the extra salt the concentration gradient for potassium ion "held" an asymmetric distribution of potassium on the B side of the membrane, and the force of the resultant equilibrium potential (Em = EK+ = 77 mV) exactly balanced the chemical gradient. Now the balance is upset.

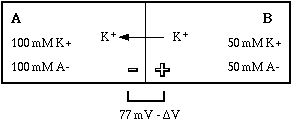
The chemical gradient has been weakened, that is, the force driving potassium from A to B has been reduced. The weakened gradient can no longer hold as much charge in compartment B, so potassium is driven into compartment A, changing the equilibrium potential by the quantity deltaV. Some of the positive ions that were separated from their negative counter-ions by the membrane are now back on the same side as their counter-ions, so fewer ion pairs are separated and the membrane is less polarized. The new equilibrium potential can again be calculated from the concentration gradient for potassium using the Nernst equation.

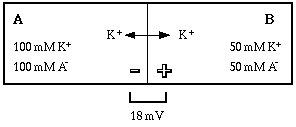
Notice that the direction of movement was toward compartment A, which has a higher concentration of potassium. How could the ion move against its concentration gradient? Remember the key word balance. With the system in equilibrium, any change in conditions must cause a response that is determined by the direction of the change.

Principle #4: When equilibrium conditions are disturbed, the direction of ion movement is determined by the direction of change, not by the direction of the concentration gradient for the ion.

Always think about the physical causes for observed effects. In the example, when the concentration gradient was weakened the "balance of power" favored the electrical potential difference. Potassium was driven by electrostatic forces against the weakened concentration gradient, until a new balance was achieved.

At this point, you might want to check out the drawings that sketch out an illustrated example of changes in membrane potential, or perhaps now is a good time to view the pretty color pictures of depolarization or hyperpolarization of a membrane.

Created by David R. Caprette (caprette@rice.edu), Rice University 17 Dec 97
Updated 15 May 09
Copyright and Intended Use