Change in Equilibrium Potential - An Illustrated Example

Pictures beat the heck out of words if you can get enough information into them without hiding the overall concept. Here is an illustration of a change in equilibrium potential between concentration cells, with more picture and less verbiage.

Starting conditions

The figure below qualitatively illustrates the distribution of ions across a semi-permeable membrane under the following conditions

"Out" and "In" are compartments of fixed volume
The membrane (shaded) is selectively permeable to the cation (+) but not to the anion (-)
The concentration of both ions is 5 mM out, and 100 mM in

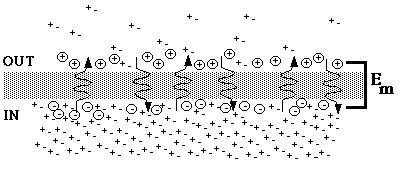
Fig. 1. Concentration cells in equilibrium

Explanation of symbols

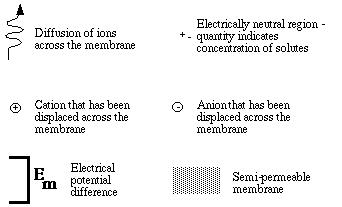
Explanation of figure 1

The figure represents an equilibrium situation. Since the membrane is impermeable to the anion, only the cation can diffuse across the membrane. At equilibrium everything is static, that is, there is no net movement in either direction, and concentrations and electrical potential difference stay the same. Nevertheless, the cation diffuses across the membrane in both directions. The two diffusion rates cancel out, so that net diffusion is zero.

The steep concentration gradient tends to drive the cation out, but the accumulating positive charge opposes that movement, so that at equilibrium positive charges are separated from their negative counter-ions and held near the outer surface of the membrane. The ions carrying the displaced charge move back and forth, but at any given instant the same amount of positive charge remains displaced across the membrane, so that the electrical force Em remains constant. The Nernst equation for the equilibrium potential for potassium accurately describes the potential difference, which in the example would be -77 mV (in compared to out).

Note that the equilibrium potential is a local phenomenon. The membrane, with its special properties, maintains a separation of charge. Get a few nanometers away from the membrane and you are in a region of electrical neutrality (equal numbers of anions and cations). In fact, the entire system is electrically neutral. Charges of opposite sign are simply held apart by the membrane.

Response to a disturbance of equilibrium

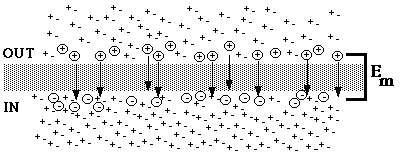
Fig. 2. Ion movement followed by a change in concentration of solute in the OUT compartment.

Suppose the concentration of solute is suddenly changed so that the concentration in the outer compartment goes from 5 mM to 50 mM. The disturbance of equilibrium weakens the concentration gradient so that it can no longer hold as much positive charge outside the membrane. A transient net movement of cations toward the inner compartment takes place. The driving force for the movement (which is against the concentration gradient) is the electrical potential difference, which is now too great to be maintained by the weaker concentration gradient.

During the equilibration period, which is of very short duration, ion flux still continues in both directions (not shown, for clarity).

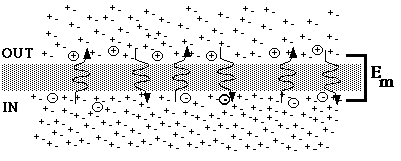
Fig. 3. Steady state following a weakening of the concentration gradient.

Figure 3 represents the new steady state. It looks a great deal like figure 1, but the concentration in the outer compartment is 50 mM instead of 5 mM, fewer charges are displaced across the membrane, and the potential difference has been reduced in magnitude.

During all of these adjustments, the concentration of the inner compartment remained exactly the same, for practical purposes. The concentration of the outer compartment was changed only when we deliberately changed the concentration. As long as there is selective permeability ion movements during equilibration do not have a measurable effect on chemical concentrations in either compartment.

At this point, you might want to check out the pretty color pictures of depolarization or hyperpolarization of a membrane, if you haven't already.

Created by David R. Caprette (caprette@rice.edu), Rice University 9 Dec 97
Updated 15 May 09
Copyright and Intended Use