Fractional Quantum Hall Effect Experiments at NHMFL (Zhang, Knuuttila)

Introduction : Fractional quantum Hall effect

In 1980, Von Klitzing discovered integer fractional quantum Hall effect (IQHE) in a Silicon MOSFET in 1980. Fractional quantum Hall effect in two dimensional electron gas (2DEG) was first observed by D. C. Tsui, H. L. Stormer, and Gossard in GaAs/AlGaAs heterojunction. The experiments of FQHE require very low temperature and the sample with a high electron-mobility. Laughlin's theory provides an excellent explanation of FQHE at filling factors 1/3, 1/5, and 1/7, where a new state of matter, an incompressible quantum liquid of electrons can exist due to electron-electron interactions. FQHE indicates the collective properties of electrons. FQHE at lowest Landau level filling factors ν=1/m (m=1, 3, 5, 7, …) indicate fractional charged quasiparticles, with charges ±e/m (minimum excitation), excited over an energy gap. The fractional quantum Hall effect appears also at other odd-denominator fractions, ν=p/q, p is an integer and q is an odd integer. The features at the hierarchical series ν=p/(2p±1) can be explained by the composite fermion (CF). Composite fermions were originally observed around filling factor 1/2. We can consider each electron in 2DEG as a magnet flux tube, the unit of quantum flux is h/e for one electron. At ν=1/2, there exists two magneto flux for each electron; the quantum unit is named composite fermion (CF), with a behavior like without external magnetic field. In the second Landau level, the even-denominator state at ν=5/2 is very intriguing, because it is the unusual FQHE state. The 5/2 state exhibits an precise plateau in Hall resistance and a deep minimum in magnetoresistance.

Magnetotransport experiments in high Landau level (N > 0) have revealed several many-particle quantum phases. Well-known examples include the even-denominator fractional quantum Hall states at filling factor 5/2 and 7/2 in the N = 1 LL, and the stripe electronic states responsible for anisotropic resistance observed at 9/2 and 11/2 in the N = 2 LL. It was found, moreover, phase transitions take place between these novel phases if certain parameters can be tuned experimentally. For example, the incompressible 5/2 quantum Hall states are found to become an anisotropic state under a tilted magnetic field [1,2].  Previous experiments were performed using high-mobility GaAs/AlGaAs heterostructure with an electron density in the range of . We report here the results for a high electron-density quantum well (QW) with an electron density  and a low-temperature mobility .

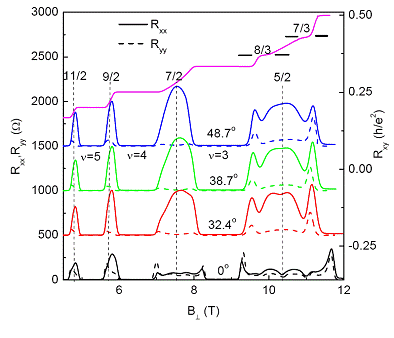
The experiments were performed using the SCM1 dilution refrigerator/superconducting magnet system; tilted magnetic field experiments were facilitated by a sample rotator.  We observe the  quantum Hall plateau at a high magnetic field 10 T. In contrast to previous findings in a lower system, electronic transport at filling factors 9/2 and 11/2 in this QW is essentially isotropic.  Anistropic transport at 9/2 and 11/2 can be induced by an in-plane magnetic field. Depending on thedirection (with respect to the GaAs crystalline axis), the  diagonal resistances in a high  either remain isotropic or become strongly anisotropic.

The 5/2 Quantized Hall plateau is observed at a magnetic field of 10 T in a high-mobility, high-electron density QW, while the resistances at 9/2 and 11/2 are essentially isotropic. The magnetotransport at these filling factors were measured in a tilted

Dr. Rui-Rui Du
rrd@rice.edu
Rice University Physics & Astronomy
Dell Butcher Hall Rm. 170
1900 Rice Blvd. Ent. 20
Houston, TX 77005

>Office Phone: 1-713-348-5780

>Lab Phone/Fax: 1-713-348-5719

References

[1] Pan, W., et al., Phys. Rev. Lett. 83, 820-823 (1999).
[2] Lilly, M. P., et al., Phys. Rev. Lett. 83, 824-827 (1999).

Fig. 1 Longitudinal resistances and are shown as a function of perpendicular magnetic field at several values of the tilt angle; the in-plane magnetic field
is applied along the high-resistance axis.  Temperature T = 50 mK.