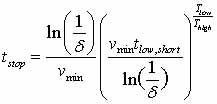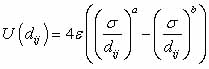Reviews
in Undergraduate Research - Issue 2
| MOLECULAR DYNAMICS AS A BRIDGE: FUNDAMENTALS, METHODS, AND
CURRENT RESEARCH
}
Kaden Hazzard
College of St. Benedict/St. John's University
Communicated By: Dr. John Wilkins
Ohio State University, Departments of Physics |
SUMMARY
Molecular dynamics (MD) is a widely
used tool in condensed matter physics, as well as other disciplines
ranging from chemistry to high-energy physics. In MD, one integrates
the equations of motion - Newton's second law for classical particles
- directly, invoking no approximations. To do so requires an interaction
potential energy or forces between atoms. I will discuss both integration
schemes and potential types. MD potentially bridges two length scales
- macroscopic and atomistic - and also links experimental results
with theories. This will be emphasized through a discussion of modern
research in solid-state physics, with each research application highlighting
a different type of interaction potential. I will discuss fluid flow
briefly and highlight some other applications of Lennard-Jones potentials,
surface growth using a Stillinger-Weber potential, and defects in
silicon using tight-binding potentials. I give some references regarding
density-functional theory calculations of these defects.
A different avenue of modern MD research
is in the method itself rather than its application. Much research
is towards developing so-called acceleration methods. By taking advantage
of the physics of condensed matter systems, acceleration methods have
been proposed which extend the time scales accessible by MD by orders-of-magnitude
in many cases. In this article, I will focus on A. F. Voter's methods,
giving their motivation, algorithm, and some derivations.
In short, this article explain why MD
is useful and where it has been used, it gives the fundamentals necessary
for understanding a MD simulation, and discusses research into MD
methods themselves, namely Voter et al.'s acceleration methods.
INTRODUCTION
Molecular dynamics (MD) is a widely
used tool in condensed matter physics, as well as other disciplines
ranging from chemistry (Kityk et al., 1999) to high-energy physics
(Bleicher et al., 1999). This article focuses on applications to solid-state
physics; however, the basic concepts presented should be valuable
to any newcomer to MD, regardless of their field.
One of MD's appeals is that the system
in consideration is simulated directly - without assuming the nature
of transitions or the types of the structures. Moreover, due to increasing
computer power, MD provides atomistic detail for system sizes that
are exponentially increasing to mesoscopic scales. Already, with classical
potentials, simulations are performed with hundreds of millions of
atoms for hundreds of picoseconds (Kadau et al, 2002) or with a more
accurate tight-binding potential simulating about 64 atoms for 0.250
microseconds (Richie et al., 2002) - nearly a timescale measurable
on a stopwatch!
Note that MD bridges two scales - macroscopic
and atomistic - and thus links experimental results, say transport
measurements, with theories governing the interactions of the simulated
matter's constituent atoms. Indeed, conventional "pencil-and-paper"
theory generally cannot evaluate the properties that are of direct
consequence in experiments. In this light, MD forms another bridge,
one between experiments and conventional theory. By iterating the
process of performing simulations and experiments, theories of forces
between atoms are refined.
With MD now appropriately evangelized,
the exposition of the fundamentals begins. Traditional (non-accelerated)
MD is conceptually simple. Using some potential interaction between
particles, Newton's second law updates the particles' velocities and
positions; repeating this, the equations of motion are integrated
and the system's trajectories are obtained. In order to be relevant
at finite temperature, pressure, etc., the system must be modified
to ensure it stays at a constant energy, temperature or in whichever
thermodynamic ensemble is desired. Methods of simulating the correct
ensemble are not given here but can be found in (Rapaport, 1997).
Before giving specific examples of research
into new MD methods (acceleration methods), I present the more technical
aspects of MD. Expositions of integration algorithms follow a background
in potentials. Accelerating MD motivates the parallel-replica, hyperdynamics,
and temperature-accelerated dynamics acceleration methods, as well
as on-the-fly kinetic Monte Carlo. Finally, illustrative research
at the forefront of MD simulation in solid-state physics is discussed;
each piece of research highlights a different class of potentials.
POTENTIALS
To accurately propagate
the system, we must have an accurate interaction potential. This potential
gives the potential energy as a function of the atomic positions and
velocities. Details on existing potentials are given, as well as some
general ways of deducing potentials.
Common Potentials
One can generally group
potentials into three basic categories: classical potentials, tight-binding
potentials, and density-functional calculations, in order of increasing
computational complexity. Representative examples are discussed:
Lennard-Jones (LJ), MEAM, and Stillinger-Weber (SW); empirical tight-binding
(TB); and density-functional theory (DFT). LJ considers interactions
between pairs of atoms; MEAM adds corrections, beyond pairwise interactions,
based on the local geometry; TB and DFT add quantum mechanics at
increasingly sophisticated levels. Each potential will be discussed
later in terms of a particular research application.
Regardless of the potential,
deriving its form requires assumptions, or the form of the potential
may just be guessed. In optimizing a potential's accuracy, parameters
are adjusted (like the balance between attractive and repulsive
LJ parameters - see below) so the potential reproduces quantities
such as lattice constants and defect energies obtained from first-principles
calculations or experiment (Baskes, 2001).
Efficient Potential
Calculations - see (Rapaport, 1997) for more information
Once the potential is
obtained, it must be computed repeatedly in a MD simulation, a O(N2)
or worse calculation, where N is the number of particles, rendering
simulation of large systems impossible. A O(N) calculation is achieved
in practice by one of two methods:
1. The "cell method"
- This method divides the system being simulated into cells, each
with a linear size larger than the interaction cutoff rc (Figure
1), where rc is a value such that atoms farther apart than this
value essentially do not interact. Now one needs only to compute
interactions between atoms in the same and adjacent cells (Figure
1), causing a speedup to O(N) for even moderate size systems.
2. The "neighbor
list method" -- In fact, only 16% of the atoms, on average,
included in the cell method are within a distance of rc (Rapaport,
1997). Hence we keep a list of all "neighbors" of an atom.
This is actually an O(N2) calculation. Fortunately, one can code
this efficiently and only compute it only once every many time-steps
since there is an upper bound to how fast things are moving, effectively
making the overall system an efficient O(N) calculation for most
system sizes.
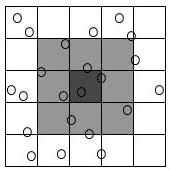 |
| Figure
1.
Two-dimensional illustration of the cell method. The dark gray
cell needs only to check the light gray cells – its nearest
neighbors – because all other atoms must lie outside of
the interaction cutoff range rc, the range beyond which no particles
interact. |
POSITION INTEGRATION
ALGORITHMS
Some details of potentials
and their calculation are now familiar. With the potential and initial
conditions Newton's second law can be integrated for all the particles.
The verlet and predictor-corrector (PC) methods are common for performing
the integration.
The integration algorithm
usually does not need to be extremely accurate. Because an extremely
slight position displacement at any time (or an equivalent round-off
error) can cause huge differences in the atom's trajectory at all
later times after a certain time, only quantities which are insensitive
to exact trajectories "matter." This is not particular to
MD, but is characteristic of the natural process itself.
The verlet method gives
positions at a short time t after the time corresponding to the supplied
positions. Each is derived in a straightforward manner from the Taylor
expansion, in time, of the atomic coordinates. The formula for the
verlet propagator is (Rapaport, 1997) .
The verlet propagator is
commonly used for its simplicity and tendency to conserve energy.
The PC methods are more
accurate than verlet, but they are not used as frequently as the simpler
verlet-class propagators. The primary advantage of the PC method over
the verlet-like algorithms is in the ability to change t on the fly,
which may be useful in systems where one set of particles inherently
move faster than others. PC is also useful when constraints (on, say,
bond length or angles) are placed on the system (Rapaport, 1997).
The PC method predicts
positions based upon Adams-Bashforth extrapolation, which is exact
if they follow monic polynomials. After prediction, correction is
made via a different set of formulae. For the (relatively complex)
equations see (Rapaport, 1997).
BETTER (FASTER!)
MOLECULAR DYNAMICS
Although MD is an increasingly
mature field, there are still continuous advances in methods. Voter
et al. have developed several methods for increasing MD's performance
by many orders of magnitude. Each method requires some assumptions
- usually forms of transition state theory (TST) (Voter, 2002 or Lombardo,
1991) - on the nature of transitions. However, the assumptions are
minimal and their validity can be checked.
There are three common
families of acceleration techniques, namely parallel-replica (PR or
par-rep), temperature-accelerated dynamics (TAD), and hyperdynamics.
The families can be utilized simultaneously for multiplicative performance
boosts. Voter gives an excellent, accessible review concentrating
on these acceleration methods (Voter, 2002).
The limitation that keeps
one from simulating long time scales is the fact that MD is a multi-scale
problem (for most solid-state systems). Specifically, one must use
a small enough integration time step to reproduce the dynamics of
the fast vibrational modes. Since these vibrations occur on the order
of 1013 - 1014 times a second, the time step for accurate integration
must be on the order of femtoseconds. A typical time step falls in
the range of 1-5 fs.
On the other hand, transitions
occur infrequently; time scales between interesting transitions range
from picoseconds (quickly diffusing surface atoms) to seconds (dislocation
motion under shearing (Haasen, 1996)). One can conceive of watching
interesting behavior for minutes or hours (for example, in crystal
growth), however the longest MD simulations can now run for only microseconds.
It must be kept in mind that the acceleration methods discussed below
only apply to infrequent event systems, systems in which the time
for transitions between 'sites' or 'structures' is much longer than
the vibrational period.
Parallel Replica
When running MD simulations
on parallel computers such as clusters one can separate the calculation
so that each processor deals only with a portion of the atoms. Thus
increasing the number of processors one can increase the size of
the simulated system. However, each processor must have many atoms
associated to it or else the communication time between processors,
rather than the computational time, will be the performance bottleneck.
While a spatial decomposition of the problem is conceptually easy,
there is no straightforward way to decompose the simulation in time
because each set of positions requires the previous positions.
To solve this problem,
Voter created the parallel-replica (PR) algorithm (Voter, 1998).
The only assumption of PR is that the probability of a system escaping
a site (transitioning from one potential minimum to another) between
times t and t+dt is given by
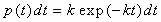 |
Eqn.
1 |
where k is the rate constant.
This is satisfied by
infrequent systems when the sites are uncorrelated (Voter, 2002).
Here uncorrelated means that once a system enters a new potential
well (crosses a saddle point in the potential energy surface) it
has no "memory" of the site it just arrived from; that
is, the dynamics after the crossing are not affected by how it got
to that site.
The PR method has been
extended to work when the probability distribution function has
a different form than Eq. 3 (Shirts, 2001). However, one must be
very careful in this case as it indicates that a "state"
is composed of several potential minima or that the runs on each
processor are not independent (see below).
With this assumption, the parallel-replica procedure can be shown
to give the same dynamics as a system simulated with non-accelerated
dynamics in the sense that the sequences of transitions from state
to state are reproduced in the long time limit. I will present how
the procedure works; for a proof, see (Voter, 2002).
To start a parallel-replica
simulation, identical systems are set up on multiple processors.
The number of processors can often be very large and consist of
many different types/speeds of processors. Now, to ensure that each
processor is simulating independent trajectories, the dynamics run
at finite temperature with momenta randomized every few time steps.
All the processors now
run dynamics until the system on one of the processors escapes from
its current state. The time elapsed on each processor is summed
and this is identified as the total time spent in the state from
which the system has just escaped. The processor that computed the
escape continues to run for a certain length of time such that after
this additional time there is no memory of the state from which
the system escaped.
The PR method solves,
to some degree, the process of parallelizing MD in the time domain.
It has been often utilized (Zagrovic B, 2001; Shirts, 2000; or Birner,
2001). Still, much the performance of the individual processors
can be increased. Hyperdynamics and temperature-accelerated dynamics
are two solutions to this problem and are discussed next.
Hyperdynamics
One (justified) way to
view the time evolution of a system is as a succession of vibrational
and transitional 'events'. This is illustrated in Figure 2; the
system oscillates in this potential well for a certain time, and
then an increase in local energy pushes the system over the transition
barrier to a new potential well (Figure 2a). Remember that this
is a high-dimensional potential well; forgetting this can misguide
intuition.
Using this picture of
dynamics, one can imagine speeding up the simulation by "filling
in" the wells (Figure 2b). However, to do this one must be
able to decide (automatically) whether the system is close to the
bottom of the well or near the transition point, since the potential
should be filled in more or less, respectively. Even assuming that
one can fill in the wells with some technique, one must map the
dynamics of the boosted system back to the non-accelerated systems.
Voter et al. describes this process in (Voter, 2002).
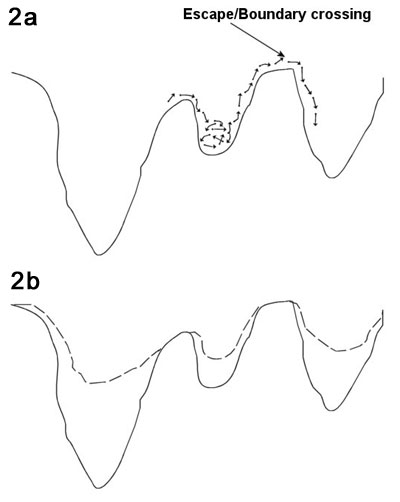 |
| Figure
2. Viewing dynamics as a sequence of vibrational and
translational events – applicable to many condensed matter
systems – and the relation to hyperdynamics. a. The particle
oscillates in its potential minimum then the energy of the system
is temporarily increased, pushing the system over an energy
barrier. b. By decreasing the depth of the potential wells,
the dynamics are sped up since less energy is required to cross
the barrier. |
As a last note, the average
boost factor for hyperdynamics is given by
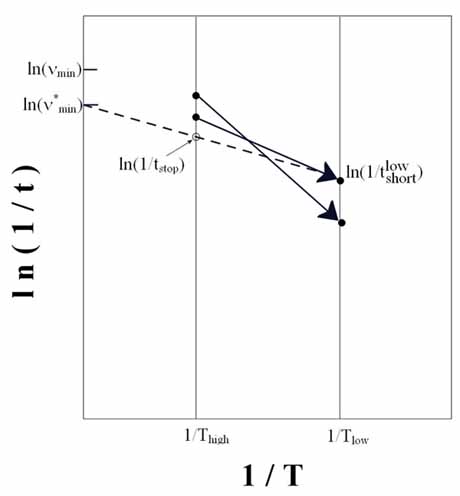
with 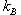 Boltzmann's
constant, T the temperature, and Boltzmann's
constant, T the temperature, and 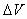 the
increase in potential energy from the bias potential. This implies
that we receive an exponentially bigger boost as the temperature
of interest lowers. Hyperdynamics has not found nearly as much success
as other acceleration methods due to technical difficulties in filling
in the potential wells. the
increase in potential energy from the bias potential. This implies
that we receive an exponentially bigger boost as the temperature
of interest lowers. Hyperdynamics has not found nearly as much success
as other acceleration methods due to technical difficulties in filling
in the potential wells.
Temperature-accelerated
Dynamics
The temperature-accelerated
dynamics (TAD) method has been more successful than hyperdynamics
to date. This method is related to hyperdynamics in that one increases
transition frequencies by making the energy barriers easier to go
over. Rather than changing the relative energetics, however, TAD
simply raises the temperature of the system.
As with hyperdynamics,
the accelerated dynamics will not directly correspond to the non-accelerated
dynamics; rather, by some a priori assumptions, the dynamics are
mapped to the lower (correct) temperature dynamics. In place of
a usual MD simulation, basin-constrained MD (BCMD) is performed
in which the system is evolved until a transition occurs. After
this is detected, the trajectory is reversed, sending the system
back into the basin from which it had just escaped. The saddle point
is calculated using, say, the nudged-elastic band method (Henkelman,
2000) and stored. This continues until a specified certainty is
reached that one possesses enough information to properly extrapolate
the dynamics to lower temperature.
Harmonic transition-state
theory (HTST) - the assumption placed on the system in this method
- states that the probability distribution for first escape times
for the basin in consideration is given by Eq. 1, with
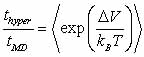 |
Eq.
2 |
where Ea is the energy
barrier the system must go over to escape from the basin, and v0
is some frequency characterizing how often the system vibrates or
attempts to leave the basin (the attempt prefactor).
Note that these equations
explain why raising the temperature changes the dynamics; changing
the temperature does not affect merely the magnitudes of each rate
constant, but affect also the relative magnitudes (hence speed up
one transition more than another). To extrapolate the transition
time from high to low temperature
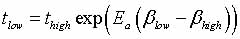 |
Eqn.
3 |
is used (Figure 3), where
tlow is the time at the low temperature and thigh is the time at
the high temperature; 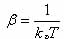 ,
and Ea is the activation energy computed by nudged-elastic band
or a related method (Henkelman, 2000). ,
and Ea is the activation energy computed by nudged-elastic band
or a related method (Henkelman, 2000).
 |
| Figure
3. Temperature-accelerated dynamics in a picture. The
system runs at high temperature until it escapes from a potential
minima and the time is then extrapolated to low temperature.
After being reflected back into the potential basin, the simulation
runs to time tstop at which point the extrapolated low-temperature
time is correct with a specified certainty. |
To derive Eq. 3, change
variables in the probability distribution (Eq. 1) to 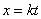 .
Then .
Then 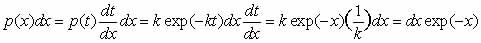 .
Hence .
Hence 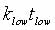 has
the same probability distribution as has
the same probability distribution as 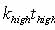 ,
and ,
and 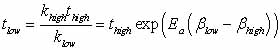 . .
This relation is illustrated
graphically in Figure 3. Here it is clear that a transition that
is not the shortest at high temperatures can be the shortest at
a lower temperature - this is why basin-constrained dynamics must
be performed. The transition with the shortest time for escape (at
low temperature) is selected as the transition corresponding to
the low-temperature dynamics and the system is updated. The BCMD
is started again from this new site. To be confident, with certainty
, that the current shortest time t0 (at low-temperature Tlow) is
correct, the system must run in BCMD for a time
where vmin is the minimum
attempt prefactor (see Eq. 2) which can be chosen manually, using
reasonable guesses; t_low,short is the shortest found time (extrapolated
to low-temperature) (Voter, 2002).
Using this technique,
one boosts the simulation speed by a factor of hundreds when interested
in low enough temperature systems (a couple hundred Kelvin). Recently,
Voter proposed a TAD enhancement (Montalenti, 2001) in which one
considers the total time spent in a state (previous and current
visit). This requires a good way of telling if two states are the
same, within symmetry, a topic just being explored in condensed
matter systems (Jiang, 2003 and Machiraju, 2003). With this improved
TAD method, the average boost factor for each state becomes
with Emin the minimum
barrier for escape from the state in consideration (Montalenti,
2001).
I briefly mention on-the-fly
kinetic Monte Carlo (OTF-KMC) simulations. KMC uses a user-specified
list of transition rates and, by sampling from the rate list, propagates
the system in time. KMC requires a priori knowledge of the transitions
and their rates, which is problematic. OTFKMC computes the list
of transitions by MD simulation (Voter, 2002) or other means (Henkelman,
2003) as the simulation progresses. When the system returns to a
state enough times, one assumes that the rate list is nearly complete
and uses KMC. To see applications of TAD and OTFKMC, see (Sprague,
2002 or Montalenti, 2002 or Montalenti, 2001).
RECENT SIMULATIONS
Lenard-Jones Potential:
Fluid Flow and Biophysics
Now I focus on current
simulations performed using MD, starting with Lennard-Jones (LJ)
potentials. LJ potentials are pairwise interaction potentials. That
is, the total potential energy of a system is just a sum over all
possible pairs i,j of atoms of a potential energy function 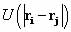 , where U is a function only of relative atomic positions of two
atoms. These interactions capture the essence of many systems, and
produce quantitatively the behavior of noble gas (say argon) liquids
and gases in many cases - the noble gases were historically very
important for the LJ potential (Collings, 1971, for example).
, where U is a function only of relative atomic positions of two
atoms. These interactions capture the essence of many systems, and
produce quantitatively the behavior of noble gas (say argon) liquids
and gases in many cases - the noble gases were historically very
important for the LJ potential (Collings, 1971, for example).
In the LJ potential there
are two parameters: one parameter governs the strength of the attractive
interaction and one of the repulsive interaction; equivalently one
can use a parameter as the potential minima depth, and another as
the atomic separation for the potential minimum ( and respectively
below). The basic formula for calculating the (LJ a-b) potential
is
Usually a=12 and b=6;
if this is the case the potential is generally just denoted LJ (rather
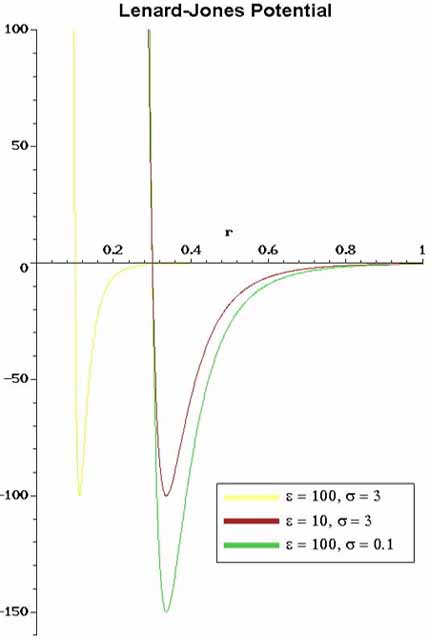
than LJ 12-6). In Figure 4 one can see the strong repulsive core
at short ranges and the weak attractive tail. The a=12 parameter
is fairly arbitrary (fortunately some physics is relatively insensitive
to the choice of a) and the value of b=6 comes from Van der Walls
attraction of non-polar substances.
 |
| Figure
4. The usual Lennard-Jones (LJ 12-6) interaction
potential. The graph is potential energy as a function of
interatomic distance. |
In addition to the noble
gases, the LJ potential is still used as part of the total potential
in biological applications (Schleyer, 1998 or Brooks, 1983). In
these situations, long-range interactions are Coulombic and LJ,
and short-range interactions (bonded atoms) obey Hooke's law. In
testing new methods, low dimensional LJ model systems are often
used. These systems have the advantage of giving qualitatively complicated
and atomic-like potential surfaces as well as, in some cases, being
analytically solvable. This, coupled with the quickness of their
simulation, gives rise to LJ's usefulness in testing models.
Moreover, the potentials
occasionally find use in condensed matter outside of biophysics.
Despite the extreme simplicity of this model, it shows many complex
phenomena characteristic of condensed matter systems (phase transitions,
complex energy landscapes, infrequent events) and hence is studied
to see the simplest examples of these phenomena (Scopigno, 2002
and Fabricius, 2002). A systematic study of large numbers of clusters
of particles interacting via LJ yields interesting results on the
dynamics and structures of these clusters, while suggesting general
features that hint at features in real clusters (Doye, 1999). Also,
when extremely large numbers of particles need to be simulated yet
a continuum approach is not applicable, such as in some fluid flow
problems, LJ is attractive. Millions of particles can be simulated
for many time steps.
As an example, Berthier
and Barrat (Berthier, 2002) have studied mixtures of sheared fluids
using a LJ potential. Two types of particles are implemented via
particle-type dependent 's and 's in the LJ potential. They are
able to investigate velocity distributions, viscosity dependence
on shear rate, and structure factors for the system at different
temperature, spanning liquid, supercooled, and glassy states. Hence,
they investigate this macroscopic system at an atomistic level of
detail, bridging these length scales as promised in the introduction.
They also correlate theoretical predictions (using a "mode-coupling
approach") with the simulations, demonstrating another of the
bridges discussed at the start. Others have used LJ to study fluid
flow as well - for a flavor, try (Bruin, 1998 or Laredji, 1996).
Classical Potentials
(beyond Lenard-Jones)
The LJ potential does
not include how the environment (nearby atoms) affects the pairwise
interaction. That is, the potential depends on terms involving three
or more relative positions, but LJ ignores this. Extra terms are
necessary to accurately simulate many systems.
Typical potentials that
incorporate these many-body interactions (in very different ways)
are modifications to LJ to include explicit angular dependence,
Stillinger-Weber (SW) (Stillinger, 1985), and the modified embedded
atom method (MEAM) (Daw, 1984). Recently, MEAM has been used to
tackle a large variety of systems; largely these have been surface
diffusion/surface growth phenomena.
Lee et al. (Lee, 1998)
and (Baskes 1997) (and many others) have studied ad-dimer (two atoms
deposited on top of a surface) diffusion on silicon surfaces. Adatom
(one deposited atom) diffusion was studied earlier (Roland, 1992).
Here I will describe results garnered by Gawlinski and Gunton (G&G)
for molecular-beam epitaxial (MBE) growth of Si(001) surfaces (Gawlinski,
1987), a simulation which involves diffusion of adatoms and ad-dimers
as well as coalescence: the clusters meet and 'stick,' forming islands.
G&G employed a SW potential for the simulation.
Some investigations have looked at the detailed mechanisms of the
diffusion of these small clusters and coalescence of these. G&G
chose to discuss only the morphology (basic shape) of the surfaces
grown and to not discuss the exact mechanisms, since classical potentials
may not properly incorporate important effects.
In MBE, atoms are deposited
(in this case as single atoms) from the gas phase onto the crystal
surface. G&G were inspired to simulate this process, in part,
by the experimental discovery of an epitaxial growth transition
temperature. Above this temperature the atoms, after striking the
surface, have time to diffuse around and find globally stable (bulk-like)
states; below this temperature, however, new atoms are deposited
close to already deposited atoms before the deposited atoms can
relax. This leads to amorphous (no local order) surface grown on
the bulk phase (Gawlinski, 1987). One of the simulation goals was
predicting this transition temperature; they succeeded in finding
a temperature in good agreement with theory (Gawlinski, 1987).
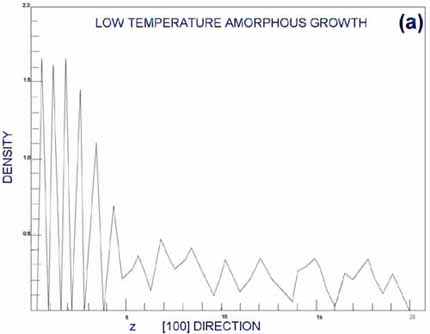
In an ordered, layered
crystal structure, the density of atoms as a function of some coordinate
should have oscillatory behavior with sharp peaks. In amorphous
structures, the density should be spread out relatively smoothly.
Figures from G&G (Gawlinsky, 1987) are reproduced as Figures
5a,b. Figure 5a is the density of deposition occurring above the
epitaxial transition temperature; Figure 5b is the corresponding
density below the epitaxial transition temperature. Clearly, the
top layers represented in Figure 5a are well layered, and in Figure
5b they seem more random. This case forms an excellent example of
MD forming the third bridge I mentioned in the introduction, that
with experiment.
 |
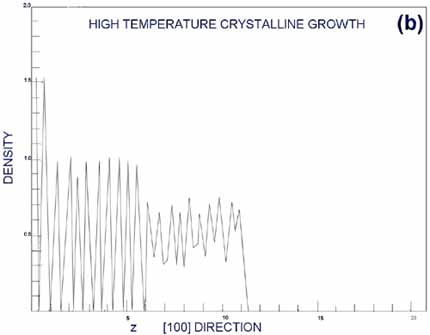 |
| Figure
5. Density of atoms as a function of depth from surface.
From (Gawlinski, 1987). a. Periodic peaks in the density profile
indicate a well-ordered, layered crystal structure. This occurs
above the epitaxial growth temperature, when individual atoms
have time to relax to bulk-like states before new atoms restrict
their movement. b. A smoother density profile at the surface
indicated amorphous surface growth, occurring below the epitaxial
growth temperature. |
While it is possible
to compare simulation results with experiment, one must be extremely
cautious in several regards. First, a simulation is only as accurate
as the potentials used, leading to the cautious interpretation above
(no detailed mechanisms). Moreover, in order to run this simulation
(in 1987, even!) the deposition rate of incoming atoms had to be
increased to extremely unrealistic values. If the time between atomic
depositions should match experiment, it is likely that no depositions
would have occurred in the time scale simulated. With this is mind,
however, something must be going correctly, or the simulation would
not have reproduced experiment.
Tight-binding Potentials
and Density Functional Theory
While purely classical
potentials have worked extremely well in some situations, often
quantum effects are important. Both tight-binding (TB) and density-functional
theory (DFT) methods incorporate quantum mechanical effects at some
level. TB incorporates these at a much less accurate level than
DFT, but TB is a couple orders-of-magnitude faster to calculate.
Moreover, TB can scale linearly with system size in some cases by
exploiting the fact that the calculation is essentially diagonalizing
a sparse matrix (Galli, 1998 or Klimeck, 2002). DFT is also widespread
in the literature, including the problem of silicon defect clusters
discussed below (for example, Kohyama, 1999; Estreicher, 1998; or
Windl, 1999). I focus on TB.
TB has found use in cluster
and defect structure and defect diffusion in some materials (Arai,
1997 or Jansen, 1988). In particular, it has been used to simulate
interstitial (extra atoms inserted between lattice sites) and vacancy
(atom removed from lattice site) clusters. Also, groups have studied
more extended structures such as the {311} defect in silicon (Kim,
2000). This is by no means an exhaustive list.
Many studies of defect
clusters in silicon are not MD simulations, but only energetic calculations,
especially in DFT. In investigations such as these, initial structures
are guessed and then the system is locally minimized (Estreicher,
1998). The downside to this is the guessing. Quite un-intuitive
structures are typical (Richie, 2002) and missed by simple guessing.
A few people (Wilkins, private communication) are advocates of performing
"cheap" TB or classical MD to explore a problem and improve
guesses for structures and transition pathways, followed by DFT
energy calculations to confirm results.
Colombo reviews TB results
of silicon defects in (Colombo, 2002). Naively, it may seem that
when an interstitial meets a vacancy, they should annihilate, leaving
only bulk silicon. This state is energetically favored, and, if
given an infinite amount of time, the system will spend most of
its time in the bulk state. However, experiments and experience
tend to deal with finite time scales on the order of seconds. Tang
et al., (Tang, 1997) find that if an interstitial and a vacancy
are placed within next nearest neighbors along the <110> direction
(in which the dimer points) then annihilation does occur. If the
vacancy and interstitial are instead separated by greater than next
nearest neighbors they do not annihilate; they attract each other
and form a stable interstitial-vacancy pair shown in Figure 6. The
energy barrier for annihilation once achieving this state is greater
than 1 eV, corresponding to a lifetime of hours for the defect at
room temperature. This strange structure is a concrete example of
why guessing structures and interaction mechanisms can fail (Richie,
2002 or Kim, 2000).
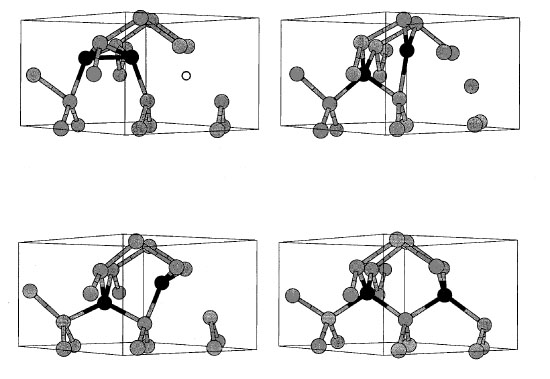 |
| Figure
6. A stable interstitial-vacancy cluster (one extra
atom, one missing atom) and its annhilation path. This unintuitive
structure (top left) is higher in energy than its lowest energy
state (perfectly crystalline), but there is a very large energy
barrier between the two states. At room temperature such interstitial-vacancy
clusters are stable for hours. |
As a final note on
this research, note that I have artificially assigned each problem
domain to a type of potential. Often, these problems do not use
the potential types I suggest. For example, hydrogen atoms effect
on Si(001) surfaces have been studied with DFT (Dongxue, 2002);
classical potentials have been used to study Si clusters (Birner,
2001); and TB potentials have been used for Ge diffusion on Si
(110) surfaces (Katircioglu, 1994). The applications I have presented
are a small fraction of all simulations performed - there is little
limit to MD's applications thanks to the lack of assumptions on
the dynamics.
CONCLUSIONS
This review does not cover
all classes of research using MD - references are representative rather
than exhaustive. However, it should have given the reader an idea
of some typical applications - fluid dynamics, surface growth, and
defect dynamics. Through examples, connections between experiment,
theory, and MD are emphasized. One now hopefully has a feeling for
the variety and advantages of some potential types.
Also one should now be
aware of some of the growing number of molecular dynamics acceleration
methods - parallel-replica, temperature-accelerated dynamics, hyperdynamics,
and on-the-fly Monte Carlo. Perhaps the most important information
presented is the necessary background to understand what goes into
an MD simulation. With this and the references, a motivated individual
could probably code a simplistic MD simulator in a matter of a week
(though given the increasing number of sophisticated, fast MD programs,
writing one from scratch is probably not advisable except as a teaching
tool).
ABOUT THE AUTHOR
Kaden Hazzard is a third-year
undergraduate at The Ohio State University planning on graduating
in the spring of 2004. He plans on pursuing a doctoral degree in condensed
matter physics. He intends to pursue a research career at a university
or at a national lab. He has been involved in computational condensed
matter physics with Professor John Wilkins's research group since
the summer of 2000. He has been researching a variety of topics, mainly
defect evolution in silicon; surface growth in silicon; and structure
recognition, characterization, and data mining of defects in solids.
He has implemented several routines in the group's multi-scale materials
simulator (OHMMS), and a new Monte Carlo method for calculating free
energies. He also spent the summer of 2002 at Los Alamos National
Labs doing low-temperature experimental work.
ACKNOWLEDGEMENTS
Everyone in Professor John Wilkin's
research group who I have had the fortune to work with deserves thanks
for their continued guidance, discussions, and ideas. In particular,
I would like to thank Professor Wilkins for his continuous suggestions
for improving this manuscript and my writing in general. I would also
like to thank Angela K. Hartsock for her gracious help with the figures.
FURTHER READING
(Rapaport, 2002) is the standard for general aspects of MD and (Voter,
2002) gives an excellent review of acceleration methods.
A
standard text regarding MD in general, along with many techniques
especially for simulations of liquids is
Allen, M.P., Tildesley, D.J. (1989) Computer Simulation of Liquids
For those interested in
finding out more about density-functional theory, a preprint for a
good review article accessible to undergraduates who have taken some
quantum mechanics, I suggest:
Capelle, K. (2003)
A bird's-eye view of density-functional theory cond-mat/0211443
REFERENCES
Arai, N., Takeda , S.,
and Kohyama, M. (1997) Self-Interstitial Clustering in Crystalline
Silicon Physical Review Letters 78 4265
Baskes, M.I. (1997) Calculation
of the behaviour of Si ad-dimers on Si(001) Modelling Simul. Mater.
Sci. Eng. 5 p. 149-158.
Berthier, L. and Barrat,
J.L. (2002) Shearing a Glassy Material: Numerical Tests of Nonequilibrium
Mode-Coupling Approaches and Experimental Proposals Physical Review
Letters 89 95702
Birner, S., Kim, J., Richie,
D.A., Wilkins, J.W., Voter, A.F., and Lenosky, T. (2001) Accelerated
dynamics simulations of interstitial-cluster growth. Solid State Communications
120 (7-8)
Bleicher, M., Zabrodin,
E., Spieles, C., Bass, S.A., Ernst, C., Soff, S., Bravina, L., Belkacem,
M., Weber, H., Stöcker, H., and Greiner, W. (1999) Relativistic
Hadron-Hadron Collisions in the Ultra-Relativistic Quantum Molecular
Dynamics Model (UrQMD) J.Phys. G25 1859-1896
Brooks, B. R., Bruccoleri,
R. E., Olafson, B. D., States, D. J., Swaminathan, S., and Karplus,
M. (1983) CHARMM: A Program for Macromolecular Energy, Minimization,
and Dynamics Calculations. J. Comp. Chem. 4, 187-217
Bruin, C. (1998) Wetting and drying of a rigid substrate under variation
of the microscopic details Physica A vol. 251, issues 1-2, pp 81-94
Chen, D. and Boland, J.
J. (2002) Chemisorption-induced disruption of surface electronic structure:
Hydrogen adsorption on the Si(100)-2x1 surface Physical Review B (Condensed
Matter and Materials Physics). vol.65, no.16 15. p. 165336/1-5.
Collings, A.F., Watts,
R.O., and Woolf, L.A. (1971) Thermodynamic properties and self-diffusion
coefficients of simple liquids. vol.20, no.6 p. 1121-33.
Colombo, L. (2002) Tight-binding
theory of native point defects in silicon. Annu. Rev. Mater. Res.,
Vol. 32: 271-295
Daw, M.S. and Baskes, M.I.
(1984) Embedded-atom method: Derivation and application to impurities,
surfaces, and other defects in metals. Phys. Rev. B 29, 6443
Doye, J.P.K., Miller, M.A.,
and Wales, D.J. (1999) Evolution of the Potential Energy Surface with
Size for Lennard-Jones Clusters. , J. Chem. Phys. 111, 8417-8428
Estreicher, S. K., Hastings,
J. L., and Fedders, P. A. (1999) Hydrogen-defect interactions in Si.
Materials Science & Engineering B (Solid-State Materials for Advanced
Technology) E-MRS 1998 Spring Meeting, Symposium A: Defects in Silicon:
Hydrogen v 58 n 1-2 p.31-5
Fabricius, G. and Stariolo,
D.A. (2002) Distance between inherent structures and the influence
of saddles on approaching the mode coupling transition in a simple
glass former. Phys. Rev. E 66, 031501
Galli, G., Kim, J., Canning,
A., and Haerle, R. (1998) Large scale quantum simulations using Tight-Binding
Hamiltonians and linear scaling methods Tight-Binding Approach to
Computational Materials Science, Eds. P. Turchi, A. Gonis and L. Colombo,
425 (1998).
Gawlinski, E.T. and Gunton,
J.D. (1987) Molecular-dynamics simulation of molecular-beam epitaxial
growth of the silicon (100) surface. Phys. Rev. B 36, 4774-4781
Haasen, Peter. (1996) Physical
Metallurgy. (Cambridge University Press) pp. 282-283
Henkelman, G., Jóhannesson,
G., and Jónsson, H. (2000) Methods for Finding Saddle Points
and Minimum Energy Paths, Progress on Theoretical Chemistry and Physics,
Kluwer Academic Publishers, Ed. S. D. Schwartz and references therein.
Henkelman, G. and Jónsson,
H. (2003), Multiple time scale simulations of metal crystal growth
reveal importance of multi-atom surface processes, Phys. Rev. Lett.
Jansen, R. W., Wolde-Kidane,
D. S., and Sankey, O. F. (1988) Energetics and deep levels of interstitial
defects in the compound semiconductors GaAs, AlAs, ZnSe, and ZnTe.
Journal of Applied Physics v 64 n 5 p.2415
Jiang, M., Choy, T.-S.,
Mehta, S., Coatney, M., Barr, S., Hazzard, K., Richie, D., Parthasarathy,
S., Machiraju, R., Thompson, D., Wilkins, J., and Gaytlin, B. (2003)
Feature Mining Algorithms for Scientific Data Proceedings of SIAM
Data Mining Conference (to appear)
Kadau, K., Germann, T.
C., Lomdahl, P. S., and Holian, B. L. (2002) Microscopic view of structural
phase transitions induced by shock waves Science. vol.296, no.5573
31 p. 1681-4.
Katircioglu, S. and Erkoc,
S. (1994) Adsorption sites of Ge adatoms on stepped Si(110) surface
Surface Science. vol.311, no.3 20 p. L703-6.
Kim, J., Kirchhoff, F.,
Wilkins, J.W., and Khan, F.S. (2000) Stability of Si-interstitial
defects: from point to extended defects Physical Review Letters 84,
503
Kityk, I. V., Kasperczyk,
J., and Plucinski, K. (1999) Two-photon absorption and photoinduced
second-harmonic generation in Sb/sub 2/Te/sub 3/-CaCl/sub 2/-PbCl/sub
2/ glasses Journal of the Optical Society of America B (Optical Physics).
vol.16, no.10 p. 1719-24.
Klimeck, G., Oyafuso, F.,
Boykin, T. B., Bowen, R. C., and von Allmen, P. (2002) Development
of a Nanoelectronic 3-D (NEMO 3-D) simulator for multimillion atom
simulations and its application to alloyed quantum dots Computer Modeling
in Engineering & Sciences. vol.3, no.5 p. 601-42.
Kohyama, M. and Takeda
(1999) S. First-principles calculations of the self-interstitial cluster
I/sub 4/ in Si, Physical Review B v. 60 issue 11, p. 8075.
Laradji, M., Toxvaerd,
S., and Mouritsen, O.G. (1996) Molecular Dynamics Simulation of Spinodal
Decomposition in Three-Dimensional Binary Fluids Phys. Rev. Lett.
Vol. 77, 2253-2256
Lee, B.J., Baskes, M. I.,
Kim, H., Cho, Y.K. (2001) Second nearest-neighbor modified embedded
atom method potentials for bcc transition metals Physical Review B.
vol.64, no.18 1 p. 184102/1-11.
Lee, G.-D., Wang, C. Z.,
Lu, Z. Y., and Ho, K. M. (1998) Ad-Dimer Diffusion between Trough
and Dimer Row on Si(100). Physical Review Letters 81 5872
Lombardo, S.J. and Bell,
A.T. (1991) A review of theoretical models of adsorption, diffusion,
desorption, and reaction of gases on metal surfaces. Surface Science
Reports Volume 13, Issues 1-2, p. 3-72
Machiraju, R., Parthasarathy,
S., Wilkins, J., Thompson, D.S., Gatlin, B., Richie, D., Choy, T.,
Jiang, M., Mehta, S., Coatney, M., Barr, S., Hazzard, K. (2003) Mining
of Complex Evolutionary Phenomena. In et al H. Kargupta, editor, Data
mining for Scientific and Engineering Applications. MIT Press.
MacKerell Jr., A.D., Brooks,
B., Brooks III, C.L, Nilsson, L., Roux, B., Won, Y., and Karplus,
M. (1998) CHARMM: The Energy Function and Its Parameterization with
an Overview of the Program, in The Encyclopedia of Computational Chemistry,
1, 271-277, P. v. R. Schleyer et al., editors (John Wiley & Sons:
Chichester)
Montalenti, F., Sorensen
M.R., Voter A.F. (2001) Closing the Gap between Experiment and Theory:
Crystal Growth by Temperature Accelerated Dynamics Phys. Rev. Lett.
87 126101 1-4
Montalenti, F., Voter,
A. F., Ferrando, R. (2002) Spontaneous atomic shuffle in flat terraces:
Ag(100) Physical Review B (Condensed Matter and Materials Physics).
vol.66, no.20 15 p. 205404-1-7.
Rapaport, D.C. (1997).
The Art of Molecular Dynamics Simulation (Cambridge University Press)
Richie, D.A., Kim, J.,
Hennig, R., Hazzard, K., Barr, S., Wilkins, J.W. (2002) Large-scale
molecular dynamics simulations of interstitial defect diffusion in
silicon Materials Research Symposium Proceedings, vol.731, p.W9.10-5
Roland, C. and Gilmer,
G.H. (1992) Epitaxy on surfaces vicinal to Si(001). I. Diffusion of
silicon adatoms over the terraces. Physical Review B 46 13428-13436
Scopigno, T., Ruocco, G.,
Sette, F., and Viliani, G. (2002) Evidence of short-time dynamical
correlations in simple liquids Phys. Rev. E 66, 031205.
Shirts, M.R. and Pande,
V.S. (2001) Mathematical Analysis of Coupled Parallel Simulations
Physical Review Letters 86, 22
Shirts, M.R. and Pande
V,S. (2000) Computing - Screen Savers of the World Unite. Science
290, 1903-4
Sprague, J.A., Montalenti,
F., Uberuaga, B.P., Kress, J.D., and Voter, A.F. (2002) Simulation
of growth of Cu on Ag(001) at experimental deposition rates Physical
Review B (Condensed Matter and Materials Physics) v 66 n 20 p.205415-1-10
Stillinger, F.H. and Weber,
T.A. (1985) Computer simulation of local order in condensed phases
of silicon Phys. Rev. B 31, 5262-5271
Tang, M., Colombo, L.,
Zhu, J., and Diaz de la Rubia, T. (1997) Intrinsic point defects in
crystalline silicon: Tight-binding molecular dynamics studiesof self-diffusion,
interstitial-vacancy recombination, and formation volumes. Physical
Review B - 1 Volume 55, Issue 21 pp. 14279-14289
Uberuaga, B.P., Henkelman,
G., Jónsson, H., Dunham, S., Windl, W., and Stumpf, R. (2002)
Theoretical Studies of Self-Diffusion and Dopant Clustering in Semiconductors,
Physica Status Solidi B, 233, 24
Voter, A.F. (1998) Parallel
replica method for dynamics of infrequent events. Physical Review
B 57 pp. 13985-88.
Voter, A.F., Montalenti,
F., and Germann, T. C. (2002) Extending the Time Scale in Atomistic
Simulation of Materials Annual Reviews in Materials Research, vol.
32, p. 321-346
Windl, W., Stumpf, R.,
Masquelier, M., Bunea, M., and Dunham, S.T. (1999) Ab-initio pseudopotential
calculations of boron diffusion in silicon. International Conference
on Modeling and Simulation of Microsystems, Semiconductors, Sensors
and Actuators 1999 p.369-72
Zagrovic, B., Sorin, E.J.,
and Pande, V.J. (2001) Beta-hairpin folding simulations in atomistic
detail using an implicit solvent model. J. Mol. Biol. 313:151-69
|



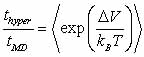

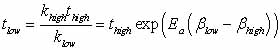 .
.