Reviews in Undergraduate Research - Issue 1

SUMMARY
In this survey of condensed matter physics, fundamental knowledge of the evolution and characteristic properties of the field will be discussed. Current trends in condensed matter physics will be identified along with their significance to the field. The reader will be exposed to research that is currently a work in progress in the sub-field of solid-state physics. The research concerns the system Ce_1-xY_xRhIn₅ where heavy-fermion, antiferromagnetic behavior and superconductivity are being explored through measurements of electrical resistivity between temperatures of 1.8 K£ T £ 300 K. Future research and technological applications from the field of condensed matter physics are also identified and explored.

INTRODUCTION
At the commencement of the 20th century, the foundations of knowledge of the macroscopic properties of matter were largely established. The fields of thermodynamics, elasticity, magnetism, and hydrodynamics collectively provided a thorough description of the "static and dynamic properties of gases, liquids, and solids at lengths long compared to molecular lengths" (Chaikin). In the 1920's, the discipline of "conventional solid state physics" emerged with the study of the quantum properties of solids (Chaiken). The areas of crystallography, elasticity, and magnetism were incorporated in the 1940's to define "solid state physics" in broader terms (Kohn). Accomplishments in the area of solid state physics have included the description of the quantum Hall effect, electronic band theory, and the detection of x-rays.
Two decades later, the 1960's, the science of condensed matter physics was introduced in an effort to study the physical properties of liquids, which resulted in an integration of the field of solid state physics (Kohn). Today, the discipline of condensed matter physics is defined as the

…fundamental science of solids and liquids, states of matter in which the constituent atoms are sufficiently close together that each atom interacts simultaneously with many neighbors. It also deals with states intermediate between solid and liquid [e.g., liquid crystals, glasses, and gels], with dense gases and plasmas, and with special quantum states [superfluids] that exist only at low temperatures. All of these states constitute what are called the condensed states of matter (Panel on Condensed Matter Physics).

The evolution of this topic is important due to its radical advances and influences in "new experimental discoveries and techniques of measurement, control of the compositions and atomic configurations of materials, and new theoretical concepts and techniques" (Kohn). An example of a paradigm introduced by CMP is "the quantum-mechanical foundation of the classical sciences of mechanics, hydrodynamics, thermodynamics, electronics, optics, metallurgy, and solid-state chemistry" (Panel on Condensed Matter Physics). The technological innovations that are attributed to CMP include and are not limited to solid state lasers and lighting, superconducting magnets, and highly sensitive detectors of radiant energy (Panel on Condensed Matter Physics).

The discovery of superconductivity occurred in 1911 through the research of Kamerlingh-Onnes (Kresin, 4). Kamerlingh-Onnes discovered that the electrical resistance of mercury abruptly vanished at very low temperatures close to 4 K (Kresin, 4). Materials that exhibit superconductivity have a characteristic critical temperature T_C. Above this finite temperature, the material acts in its normal state and displays resistance, which is "the flow of electric current that accompanies the development of heat and the dissipation of energy" (Owens, 25). Below the T_C, the material enters a superconducting state where there is no electrical resistivity [material conducts electricity without losses] (Owens, 25). The characteristics of superconducting materials are not limited to the absence of electrical resistivity. They also include "anomalous magnetic, thermal, and other properties, so it is more precise to talk…(about superconductivity as) a peculiar state of matter observed at low temperatures" (Kresin, 5). In 1933, William Meissner showed that materials in their superconducting state displayed the property of perfect diamagnetism, the "complete expulsion of a weak magnetic field from the interior" (Kohn, S72). It was not until 1986 that high temperature (high T_C) superconductivity was discovered (Owens, 25). Today's studies have yielded high T_C's of up to 160 K, but the mechanisms behind this phenomenon remain to be a mystery- as does the "experimentalist's dream" of room temperature superconductors (Kohn, S73).

In 1964, the Japanese theoretical physicist Juan Kondo was successful in explaining the effect of a localized impurity spin on the scattering of conduction electrons at low temperatures (Kohn, S68). This phenomenon, now identified as the Kondo Effect, is briefly described in terms the Kondo temperature (T_K). At T_K, the conduction electrons in a metallic, non-magnetic material respond to the addition of a magnetic impurity atom by creating a magnetic shield that offsets the introduced magnetization. For T«T_K, the shield consists of a "singlet state with the conduction electrons" and causes a disappearance of the magnetic susceptibility (Kohn, S68).

The exploration of condensed matter energy states in the 1980's contributed to the interest in a new class of metals and systems called heavy-fermion systems. These materials are depicted as possessing electronic states that have "characteristic energy orders of magnitude smaller than [those] in ordinary metals " (Fisk/Ott). Numerous heavy-fermion systems are "intermetallic compounds in which one of the constituents is a rare-earth or actinide atom, with partially filled 4f- or 5f- electron shells" (Fisk/Ott). At high temperatures, heavy-fermion materials tend to behave as if the f-electrons are localized in their atomic states like conventional paramagnets in which the moments are random and tend to want to line up with the induced magnetic field (Fisk/Ott). At low temperatures, some of the f-electrons of the heavy-fermion system tend to become itinerant and order spontaneously with mostly antiferromagnetic- moments align by periodically alternating directions-, or less frequently ferromagnetic- moments align parallel-, properties (Fisk/Ott).

On an elementary level, the building blocks of condensed matter are formed through the logical combining of "electrons and nuclei to atoms and molecules" in large quantities (~10²⁴/cm³) (Panel on Condensed Matter Physics). The crystal lattices of these systems are considered to be either periodic or non-periodic. Periodic crystal lattices occur for simple systems of crystalline solids on an atomic scale (Kohn, S69). Non-periodic lattices are easily attainable in extensive systems where defects occur within in the materials due to fluctuations in temperature (Kohn, S68). Substitution alloys compose a class of relatively non-periodic systems and are denoted by the generic formula AxBx-1 (Kohn, S69-70). The elements A and B are selected such that the elements possess identical valences [number of electrons occupying the outermost energy levels], matching crystal structures [in their pure form], and similar atomic radii (Kohn, S69-70). The Experimental section of this paper will utilize the substitution alloy relationship by discussing the elements Cerium and Yttrium in experimental context.

RECENT DISCOVERIES

Superconductivity of Buckyballs
Experimental research in the area of condensed matter physics during 1990 led to the discovery of buckyballs (Levi, 15). A buckyball is a spherical molecule composed of 60 carbon atoms that is easily manufactured in large quantities through simple techniques (Levi, 15). By 1991, "a crystal of C₆₀ molecules had been found to superconduct when doped with alkali metals atoms, which cede electrons to the C₆₀ lattice" (Levi, 15). Doping results in a material that either adds extra electrons to the material (which is then called N-type for the extra negative charge carriers) or creates "holes" in the material's crystal structure (which is then called P-type because it results in more positive charge carriers). In January of 2001, Jan Hendrik Schön, Christian Kloc, and Bertram Batlogg of Bell Labs, Lucent Technologies, discovered a new method of "injecting holes directly into the top layer of a C₆₀ crystal without adding any ions to it" (Levi, 15). In addition, the experimenters explored the behavior of the buckyball crystal by varying a continuous doping level from positive to negative values (i.e. adding less holes, positive charges, to a material and increasing the number of electrons to yield a more negative charge).

The endeavors by the Bell Labs trio led to the discovery that the hole-doped (positive charged) C₆₀ crystal had a maximum critical temperature of 52 K at a doping level between 3.0 and 3.5 holes per molecule (Levi, 15). In comparison to the negative charge injection near 3 electrons per molecule, the critical temperature (T_C) of the C₆₀ material was only 11 K (Levi, 15). These results are important to the study of superconductivity in buckyballs for two main reasons: 1. the peaking of the T_C for negative charge and hole doping of three electrons per molecule or three holes per molecule emphasizes that superconductivity favors the structure of 3 electrons per molecule, or A₃C₆₀ where A is an alkali atom; 2. "hole doped C₆₀ crystals turned out to be better superconductors than their electron-doped cousins" with much larger ranges of superconductivity (Levi, 15).

Continued research on the carbon-60 materials has led experimentalists to the realization that doping with larger atoms tends to expand the crystal lattice (Levi, 15). The resultant expansion thus causes broader spacing which "further reduces the overlap between the electron bands of adjacent molecules and narrows the bandwidths" (Levi, 15). The T_C affects the lattice through an inverse relationship with the bandwidth, the larger the doping atom, the higher the T_C (Levi, 15).

In January of 2001, the primary objective of the Bell Labs trio was to "incorporate interstitial ions that [would] expand a hole-doped C₆₀ lattice" and hopefully raise the T_C well above 100 K (Levi, 15). In a time period of just nine months, the team was successful in accomplishing their goal as the T_C of the carbon-60 crystal was made to superconduct at a temperature of 117 K. The researchers were successful is raising the T_C as a result of a new approach, electronic hole-doping with "neutral molecules to [assist in] expand[ing] the crystal [lattice]" (Levi, 19). The neutral molecules, tribromomethane (CHBr₃), caused an expansion in the cubic lattice constant from 14.16 Å to 14.43 Å and a T_C of 117 K (Levi, 21). (A cubic lattice is generally described in terms of a unit cell with a cubic structure. The cubic structure includes three primary lattice vectors of equal magnitude (i.e. equal sides) and angles of 90° between each edge. The magnitude of the lattice vectors (i.e. length of each side) is referred to as the lattice constant.) Comparatively, when CHCl₃ was used as a neutral molecule, the T_C was only 80 K (Levi, 21). Experimentalists at Bell Labs are now searching for other neutral molecules that will expand the lattice constant in order to reach superconducting critical temperatures of 150 K (Levi, 21). If feasible, the future of thin-film electronics will benefit immensely (Levi, 21). Overall, the discovery of superconducting buckyballs is important, according to Robert Cava of Princeton University, because it means that thermodynamics is the only thing that has prevented physicists from unearthing more 100 K plus superconductors (Levi, 21).

Ferromagnetic Superconducting Material
A superconducting state is produced through lattice vibrations in low T_C materials or through magnetic fluctuations in high T_C materials that tend to push electrons together and expel any existing magnetic fields (Day, 16). Roughly one year ago, Gil Lonzarich's group at the Cambridge University and their collaborators at Grenoble's Atomic Energy Commissariat discovered that UGe₂, an alloy of uranium and germanium, "exhibited superconductivity and ferromagnetism simultaneously" (Day, 16). Now, another ferromagnetic superconductor, ZrZn₂, has been found to exist through the research of Christian Pfiederer of the University of Karlsruhe (Day, 16).

The compound ZrZn₂ is interesting because each component is paramagnetic, but together the system displays weak ferromagnetism with a Curie temperature, T_m, of 25 K (Day, 16). This point marks the "highest temperature at which magnetic order prevails" (Day, 16). When Pfiederer studied the samples of ZrZn₂ at varying pressures, he found that the compound had a superconducting transition at ambient pressure and at pressures lower than the critical pressure (Day, 17). The temperatures T_C and T_M were found to fall linearly in pressure from their ambient values until each vanished at the same critical pressure of 2.1 GPa (gigapascals) (Day, 17). The data presented above shows "strong evidence that the same electrons mediate both superconductivity and ferromagnetism. The high critical pressure indicates that superconductivity in ZrZn₂ occurs firmly in the ferromagnetic state, rather than close to the quantum critical point" (Day, 17). The study of ferromagnetic superconducting systems is hoped to lead to scientists to understand the phenomenon behind the high T_C superconductors (Day, 16). Also, the information gathered from the UGe₂ and ZrZn₂ systems strongly suggests that superconductivity is no longer an isolated phenomenon, but a generic effect caused by magnetic fluctuations (Day, 18).

EXPERIMENTAL

What and Why?
Recently, it was discovered that heavy-fermion systems exist in Ce-based compounds with the structure CeRhIn₅ (Thompson). Specifically, the compound CeRhIn₅ is a heavy fermion system which displays antiferromagnetism but does not superconduct at ambient pressure. The Maple Lab at the University of California at SanDiego is currently exploring the compound CeRhIn₅. The nonmagnetic element Yttrium, Y, was added to the compound, CeRhIn₅ to yield the compound Ce_1-xY_xRhIn₅, thus diluting the Ce magnetic moments. The element Yttrium was chosen because of its nonmagnetic properties and ability to be a substitution alloy in conjunction with the element Ce. Yttrium and Cerium are substitution alloys for three reasons: 1. each possesses three valence electrons (Cerium possesses 3 valence electrons at ambient room temperature and pressure. However, when subject to cooling or compression, the valency changes from about 3 to 4.); 2. the atomic radii are similar with Ce=2.7Å and Y=2.27Å; 3. in their pure form both Ce and Y have a close packed hexagonal structure. The objective of studying the system Ce_1-xY_xRhIn₅ with 0£ x £ 1 was to explore the magnetic phase diagram, and to search for possible non-Fermi liquid behavior at a quantum critical point where the Néel temperature, TN, is suppressed to near 0 K or very low temperature ranges. The Néel temperature is the critical temperature of an antiferromagnetic material above which paramagnetism occurs.

Experimental Details
Single crystals of the intermetallic compound form Ce_1-xY_xRhIn₅ were prepared and grown using a molten In flux technique in alumina crucibles, which were sealed under vacuum in quartz tubes. The molten Indium flux technique requires that the Indium surround the starting materials (with the higher melting temperatures on the bottom) inside the crucible. As the low-melting materials melt they flow over the higher-melting materials and incorporate them into the melt. The crucibles were heated inside a furnace to a temperature of ~1100°C for 24 hours and then cooled slowly (at ~5°C/hour) to 600°C. The samples were then removed from the furnace, immediately inverted, and centrifuged at room temperature, in an effort to remove the molten Indium.

In order to ensure the correct structure of each sample, powder diffraction x-ray data was taken. The peaks from the experimental data were then plotted and compared against those of the known theoretical CeYRhIn₅ and Germanium peaks. Once all of the major peaks from the sample were accounted for, it was concluded that the correct crystal lattice structure had formed. If significant peaks existed in the experimental data that were not categorized as concentrations of In, Ge, or CeRhIn₅, the sample was assumed to contain impurities. The lattice constants for each compound were determined by comparing the angles of the experimental peaks to the indices and angles of the simultaneous theoretical peaks. Then XLAT, a Least Squares (LSQ) program, used the resultant theoretical indices and experimental angles to calculate the precise refinement of lattice constants (a, b, c) in units of Angstroms. The lattice constants for the Ce_1-xY_xRhIn₅ data were calculated for a tetragonal lattice system where a = b ¹ c.

Resistivity was measured as a function of temperature in a ⁴He cryostat. (Usually neutron diffraction measurements are necessary to determine the magnetic structure of the compound. Resistivity provides us with a hint, as we can postulate that there might be a Néel temperature if we see a kink.) The resistivity slices were prepared by attaching gold leads to the sample with silver epoxy. Temperatures in the range of 1.8K to 300 K were generated for each resistivity slice (preferably long, thin rectangular crystals of the sample) within the Ce_1-xY_xRhIn₅ system being studied. Once the resistivity slices were placed into the 4He cryostat, a magnetic field of 300 Oe was applied to overcome Indium's superconducting state and a maximum current flow of 10mA with a 16 Hz frequency was produced in order for the resistivity slice to reach low temperatures without interference.

RESULTS

Crystal Formation
X-ray diffraction measurements reveal whether or not a specific compound of the type Ce_1-xY_xRhIn₅, 0 = x = 1, has formed the correct tetragonal crystal structure. The graphical representations of the x-ray diffraction measurements for Ce_.1Y_.9RhIn₅ are located in figure 1 and 2, with 2 representing a zoomed view. The plot consists of experimental Ce_.1Y_.9RhIn₅ and theoretical Ge, CeRhIn₅ data for intensity (counts) vs. angle (q). The peaks in the plots result from variations in intensity where "for only certain values of q will the reflections from all parallel planes add up in phase to give a strong reflected beam"- specular reflection (Kittel). A calibration standard, Germanium, was used to reveal phase shifts in the experimental peaks relative to CeRhIn₅ by mixing powdered Germanium with the powdered sample, x-raying the two substances, and comparing the known location of the theoretical Ge peaks with those from the experimental sample. Upon a close analysis of Figure 1 it is apparent that all of the major experimental peaks are accounted for by the theoretical data. Hence it can be easily determined that the sample compound Ce_.1Y_.9RhIn₅ formed the correct tetragonal crystal lattice structure. Similar processes and graphical representations were used to ensure that each compound of the Ce_1-xY_xRhIn₅ system formed the tetragonal crystal structure.

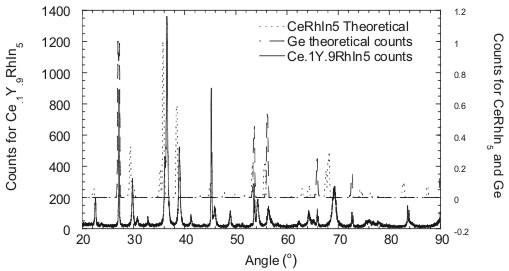Figure 1. Graphical representation of the x-ray diffraction measurements for Ce.1Y.9RhIn5 against CeRhIn5 theoretical and Germanium theoretical. The graph is plotted as intensity vs. theta for 20° £ q £ 90°.

 

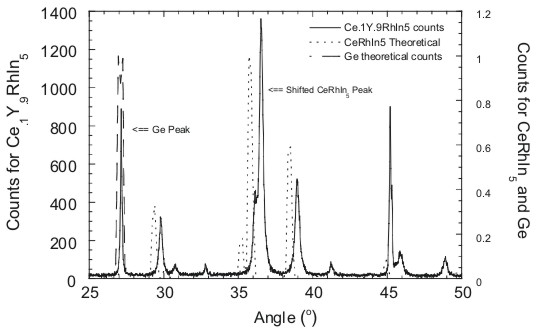Figure 2. Magnified version of the graphical representation of the x-ray diffraction measurements for Ce.1Y.9RhIn5 against CeRhIn5 theoretical and Germanium theoretical. The graph is plotted as intensity vs. theta for 20°£ q £ 50°.

 

Crystal Parameters
The x-ray diffraction measurements reveal that the crystals formed in the tetragonal CeRhIn₅ structure. The lattice constants for the Ce_1-xY_xRhIn₅ system are a and c. These are plotted as a function of x, Yttrium concentration, in figures 3 and 4. A linear relationship should exist between the concentration of the substitute element and the size of the lattice parameters, which is called Vegard's Law. The direction of the linear relationship, increasing or decreasing, depends upon the system being analyzed. The graph for lattice constant a follows the rules set forth in Vegard's law. Figure 3 shows that as the concentration of Yttrium is increased, lattice constant a decreases, implying the cell is contracting along the a axis.

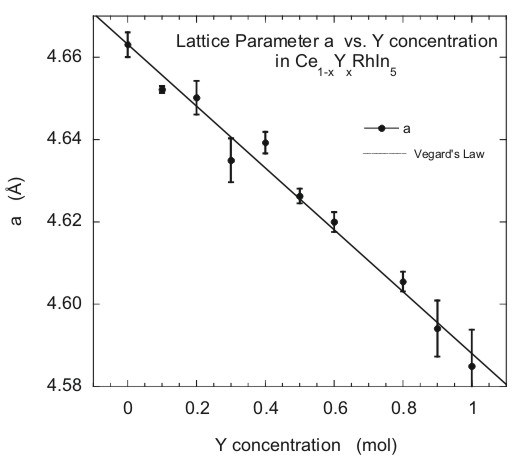Figure 3. Tetragonal lattice constant a as a function of Y concentration x for the Ce1-xYxRhIn5 system. The dotted line is a fit to the data and the solid line represents the linear relationship of Vegard's law.

 

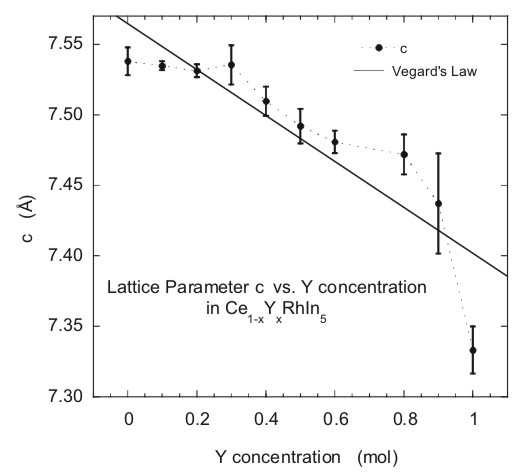Figure 4. Tetragonal lattice constant c as a function of Y concentration x for the Ce1-xYxRhIn5 system. The dotted line is a fit to the data and the solid line represents the linear relationship of Vegard's law.

The graph for the c lattice parameter is shown in Figure 4. The relationship between the size of the c parameter and the concentration of Yttrium does not obey Vegard's law. Instead, the curve appears constant for 0 £ x £ 0.3, and then a decreasing linear dependence occurs on x for x ³ 0.3. Overall, the results from Figures 3 and 4 provide evidence for a contracting cell structure along the a, b, c axes (where b = a) as the larger Yttrium ion is substituted on the Cerium site.

Electrical Resistivity
The normalized electrical "resistivity," r/r(300K) vs. T of various Ce_1-xY_xRhIn₅ compounds is displayed in Figures 5 and 6. Figure 5 compares the resistivity for concentrations of .2 £ x £ .8 while Figure 6 displays that of x=1 and x=. 9. The resistivity for .2 £ x £ .8 are weakly temperature dependent for temperatures above ~100 K. Below ~100 K a considerable decrease in slope tends to occur with a hump around ~50 K. For T<50 K there is a rapid decrease in r(T) with decreasing T. This decline is caused by the onset of coherence in the Cerium ion sublattice. The end member compound CeRhIn₅ exhibits similar behavior to the concentrations of .2 £ x £ .8. Upon close examination of the slopes in Figure 5, there is no consistency, as the slopes do not decrease nor increase with increases in the concentration of Yttrium.

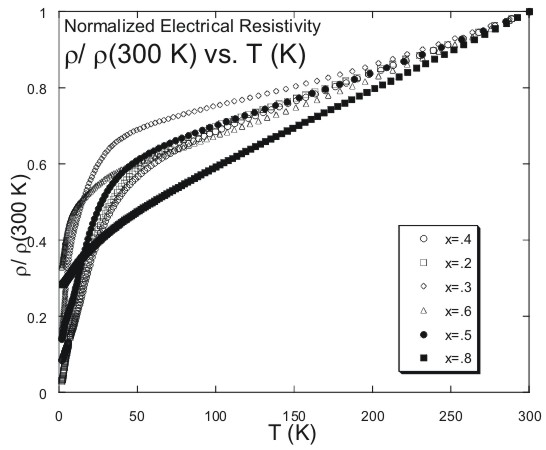Figure 5. Electrical resistivity r normalized to its value at 300 K, r/r(300 K), as a function of temperature for Ce.1Y.9RhIn5 with .2 £x £.8 and x = .8.

 

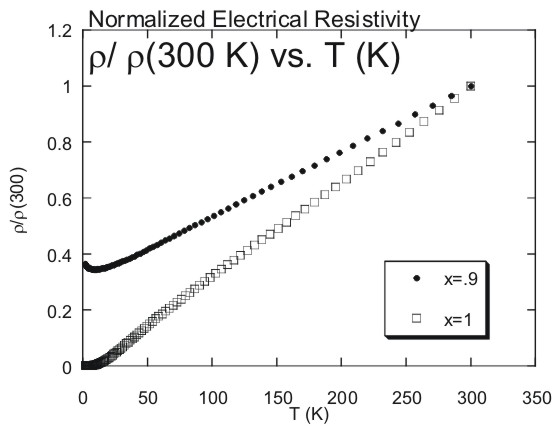Figure 6. Electrical resistivity r normalized to its value at 300 K, r/r(300 K), as a function of temperature for Ce.1Y.9RhIn5 with x = .9 and x = 1.0.

The concentrations of x displayed in Figure 6 exhibit behavior that is different from those of the other x concentrations. The resistivity of the curves for x=0.9 and x=1 are weakly temperature dependent for temperatures above ~100 K. Below ~100 K a rapid decrease occurs in r(T) with decreasing T. A minimum occurs at ~20 K for x = 0.9 and then a slight increase in resistivity occurs for T< 25K. For x=1, YrhIn₅, r(T) decreases rapidly until ~50 K and then begins to level off slightly for T < 50 K. The graphs of resistivity for 0£ x £ 1 do not display the Néel temperature where the onset of antiferromagnetism may occur as in some systems a kink is seen in the resistivity at the Néel temperature. It is suspected that antiferromagnetic ordering will occur for T< 1.8 K. The graphs do reveal the presence of the Kondo effect. Figure 5 displays an increase in resistivity, upturn in the curve, for T< 1.8 K while Figure 6 reveals a definite increase for x = 0. 9. There are no magnetic ions in YRhIn₅, x = 1.0, which result in a lack of the Kondo effect. There is no presence or implication of superconductivity revealed in the resistivity data for 1.8 K £ T £ 300 K. The samples with x = 0.4, 0.5, 0.6 have linear r vs. T relationship, whereas Fermi-liquid theory predicts a T² temperature dependence of the resistivity. The possibility of non-Fermi liquid behavior in these samples needs to be explored further with specific heat and magnetization measurements.

CONCLUSION
The structure of the Ce_1-xY_xRhIn₅ system was characterized by tetragonal powder diffraction x-ray measurements. The lattice parameters of this system were shown to decrease with increasing concentrations of Yttrium under ambient pressure and temperature. This provides evidence for a contracting cell structure. Measurements of electrical resistivity for 1.8 K £ T £ 50 K provide evidence of the Kondo effect. The experimental results offer no evidence of superconductivity.

Further investigation of the Ce_1-xY_xRhIn₅ system should include tracking the suppression of the Néel temperature with increasing Yttrium by means of specific heat and neutron scattering measurements. Also, the physical properties of resistivity, specific heat, magnetic susceptibility, and nuclear magnetic resonance should be investigated at low temperatures in the vicinity of the quantum critical point, T_N, to determine if non-Fermi liquid behavior is observed. A detailed investigation of these systems should enhance our understanding of the interplay of magnetism, superconductivity, and non-Fermi Liquid behavior in correlated electron system.

FUTURE POSSIBILITIES FOR RESEARCH AND APPLICATION

Polymeric Carbon-60
Recently, a collection of experiments has revealed ferromagnetic behavior in polymerized C₆₀ at temperatures near 500 K (Levi). Scientists are skeptical of this discovery because the "constituent molecules have no magnetic moments" (Levi, 18). Further investigation into this system is necessary in order to explain how and why a system composed solely of carbon can be magnetic if there are no unpaired electrons (Day, 18). Other research interests in carbon lie in the possible industrial aspects of the material. Companies are interested in finding a molecular-based material that can be cheaply manufactured and easily modulated (Levi, 18). However the samples and testing are costly (Levi, 18).

Solid State Lighting
A dilemma that is becoming more widespread every year is the challenge of generating electricity. The process is becoming more costly economically and environmentally as the years progress. The current state of lighting focuses mainly on incandescent and florescent sources (Bergh, 42). However, lighting applications that use Light Emitting Diodes (LEDs) and Organic Light Emitting Diodes (OLEDs), commonly referred to as Solid-State Lighting (SSL), are being developed. In SSL, a semiconductor converts electricity to light. The life of the device depends on packaging considerations, drive current, and the operating environment (increased temperatures produce lower light output). SSL offers economic and environmental savings over the current incandescent sources through long life, high efficiency, low voltage, and vibration and shock resistant. It is proposed that with SSL the US would be able to reduce lighting expenditures between 2000-2050 by $100 billion and spare 28 million metric tons of carbon emission into the atmosphere annually (Bergh, 42).

Other benefits of SSL include variety, aesthetics, and durability. The circuitry of SSL allows for control over the size, color, intensity, and design, thus resulting in light coloring similar to that of the sun and allowing physical features such as "flat packages of any shape that can be placed on floors, walls, ceilings, or even furniture" (Bergh, 42). Overall, SSL offers consumer friendly advantages that will revolutionize light sources over the next few decades.

ABOUT THE AUTHOR
Kristen Rogers is a junior at Emory University where she is pursuing a bachelor of arts and science in both physics and mathematics. Upon graduation in May 2003, Kristen intends to pursue a PhD in one of the areas of experimental physics. Her final career goal is to develop national security technology for the United States Navy.

The research that Kristen conducted during the summer of 2001was completed through the REU program offered at the University of California at San Diego. There, she worked in the Maple Condensed Matter lab under the supervision of professor M. Brian Maple and graduate student Vivien Zapf.

Kristen concentrated her interests in low-temperature solid-state physics. The focus of her research was on the heavy fermion system Ce_1-xY_xRhIn₅. This compound was of particular interest due to its display of antiferromagnetic behavior and lack of superconductivity at ambient pressure. Kristen participated firsthand in preparing the samples of the compound Ce_1-xY_xRhIn₅ with varying concentrations of Ce and Y. She also acquired experience in measuring the magnetic properties of these compounds at temperatures as low as 1.8K and in magnetic fields of approximately 300 Oe. The ultimate goal in studying Ce_1-xY_xRhIn₅ was to determine if the same antiferromagnetic, heavy fermion activity would be exhibited as that in the compound CeRhIn₅ when slowly adding Y and subtly eliminating Ce to the compound. The results, thus far, imply that antiferromagnetic behavior does exist and competition occurs at low temperatures between the Kondo effect and antiferromagnetism. This project is currently undergoing extensive research at UCSD. However, Kristen will no longer be an active participant due to academic obligations in Atlanta.

ACKNOWLEDGEMENTS
I would like to thank Professor M. Brian Maple, UCSD Physics Department, and the National Science Foundation 2001 Research Experience for Undergraduates program for enabling me the opportunity to partake in innovative, exciting physics research. I would also like to thank each member of the Maple lab for his/her kind support. In particular, I am especially grateful to Vivien Zapf for all the time and patience she devoted to my education, equipment know-how, and pestering questions.

FURTHER READING

1. Fisk, Z., Hess, D.W., Pethick, C.J., Pines, ., Smith, J.L., Tompson, J.D., Willis, J.O. (1988). Heavy-Electron Metals: New Highly Correlated States of Matter. Science, Vol 239.

2. Curro, N.J., Hammel, P.C., Pagliuso, P.G., Sarrao, J.L., Thompson, J.D., Fisk, Z. (2000). Evidence for spiral magnetic order in the heavy fermion material CeRhIn₅. Physical Review B, Vol. 62, No. 10.

3. Kittel, Charles. (1995). Introduction to Solid State Physics. (ed. 7 New York, New York: John Wiley and Sons Inc).

4. Kresin, Vladimir Z., Wolf, Stuart A. (1990). Fundamentals of Superconductivity. (New York, New York: Plenum Press).

REFERENCES

Bao, Wei. Pagliuso, P.G., Sarrao, J.L., Thompson, J.D., Fisk, Z. (2001). Magnetic Structure of heavy fermion Ce2RhIn8. yet to be published, references to be cited therein.

Bergh, Arpad, Craford, George, Duggal, Anil, Haitz, Roland. (2001). The Promise and
Challenge of Solid State Lighting. Physics Today. Vol 54, No. 12, 42-47.

Chaiken, P.M., Lubensky, T.C. (1995). Principles of Condensed Matter Physics. (New
York, New York: Press Syndicate of the University of Cambridge) xvii.

Day, Charles. (2001). Second Material Found that Superconducts in a Ferromagnetic
State. Physics Today. Vol. 54, No. 9, 16-18.

Fisk, Z., Ott, H.R., Rice, T.M., Smith, J.L. (1986). Heavy-Electron Metals. Nature. Vol.
320, No. 37, 1.

Kittel, Charles. (1967). Introduction to Solid State Physics, ed. (New York, New York: John Wiley and Sons Inc) 37, 38, 42.

Kohn, W. (1999). An Essay on Condensed Matter Physics in the Twentieth Century.
Reviews Of Modern Physics. Vol. 71, No. 2, S59, S68-70, S72.

Kresin, Vladimir Z., Wolf, Stuart A. (1990). Fundamentals of Superconductivity. (New
York, New York: Plenum Press) 4, 5.

Levi, Barbara Goss. (2001) BuckyBalls Found to Conduct at 52 K. Physics Today.
Vol. 54, No. 1, 15-16.

(2001) Buckyball Crystals Made to Superconduct at 117 K.
Physics Today. Vol. 54, No. 10, 15-16.

(2001) Can Polymeric Carbon-60 Be Magnetic? Physics Today.
Vol. 54, No. 12, 18-19.

Owens, Frank J., Poole, Charles P. Jr. (1997). The New Superconductors. (New York,
New York: Plenum Press) 25.

Panel on Condensed Matter Physics, Physics Survey Committee, Board on Physics and
Astronomy, Commission on Physical Sciences, Mathematics, and Resources, National Research Council (US). (1986). Condensed-Matter Physics. (Washington, D.C.: National Academy Press) 3.

Thompson, J.D., Movshovich, R., Fisk, Z., B ouquet, F., Curro, N.J., Fisher, R.A.,
Hammel, P.C., Hegger, H., Hundley, M.F., Jaime, M., Pagliuso, P.G., Petrovic, C., Phiilips, N.E., Sarra, J.L. (2000). to appear in J. Magn. Magn. Mat. (2000), references cited therein.