Acalculia and Language

There is a strong relationship between acalculia and language.  A good example of this is observed in children who can do basic number related tasks when they are young.  They become significantly better, however, when language develops (Cohen et al, 1999). 

Why?

Children are now able to form and assign verbal labels to quantities, manipulate number symbolically now and some parts of numerical calculations are a direct result of verbal abilities (Cohen et al., 1999).

Does language and numerical calculation lie in the same hemisphere? (Semenza et al., 2006)

A study by Semenza et al. in 2006 tried to determine exactly this.  They performed the study a group of 6 crossed aphasics and 2 left handed right hemisphere aphasics.  Cross aphasia was first ascribed to those aphasics who had a lesion in the cerebral hemisphere that was ipsilateral to their dominant hand.  Modernly, however, crossed aphasia is exclusively used to describe those right handed aphasics who have a right hemisphere lesion.  Crossed aphasia is a general term to describe how a lesion is related to handedness but it does not replace the common types of aphasia that describe symptoms.  If you look at the table below you can see that the crossed aphasics are also classified by another type of aphasia (Broca, Wernicke, etc.).

In this study the crossed aphasics showed no signs of a lesion in their left cerebral hemisphere.  Also, all the aphasics were clearly acalculic but all to a slightly different degree.

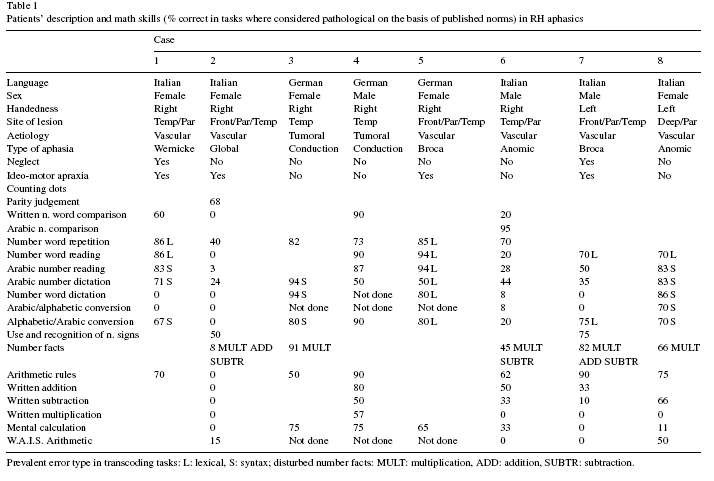
Table 1 from Semenza et al., 2006.

Semenza et al. showed that language and numerical abilities do in fact reside in the same cerebral hemisphere.  They also found that this was regardless of the location of language in the brain (either hemisphere).  Therefore, some math processes will still be retained by the original hemisphere but some numerical abilities are lateralized with language (Semenza et al., 2006).

Case Study: Patient ATH (Cohen et al., 1999)

Patient ATH is a female with a lesion in the left perisylvian area as a result of a left hemisphere infarction. 

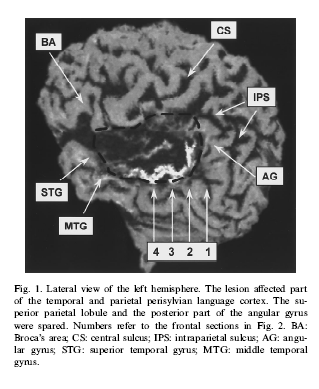
Fig. 1 from Cohen et al., 1999.

Along with suffering from aphasia and deep dyslexia, patient ATH was also determined to be severely acalculic.  ATH showed defects in many oral number tasks.  Verbally, there was trouble counting past the number 10 and also when solving an arithmetic problem, ATH would write down the correct number but blurt out an incorrect number (eg, write 12 but say 16).  Also, ATH was unable to do multiplication or remember multiplication tables.  The authors explained that the way we retrieve multiplication tables is most like verbal retrieval.  It is most interesting that there was preserved numerical calculation ability when no verbal coding of numbers was involved.  Patient ATH's case clearly shows that there is a obvious connection between language and numerical processes.

Case Study: Patient PN - Does acalculia always occur with a language deficit? (Grana et al., 2006)

The studies above only examined cases of acalculia associated with aphasia.  Acalculia can exist alone without a language deficit as observed in patient PN, a male who had an exclusively right hemisphere lesion.  The damage was a result of a hemorrhage due to a right middle cerebral artery aneurysm.  He had preserved basic mathematical operations but was unable to do multiplication. 

In the case study of patient ATH (Cohen et al., 1999), the authors explained that multiplication was most like verbal retrieval but patient PN has no language deficit.  There was no sign of aphasia in production or comprehension.  These two cases contradict each other and differneces can attributed to the complexities of the brain.

Grana et al. explain that the inability to do multiplication is due to PN not knowing where to do the problem.  That is, he knew what, when and how to do the problem but lacked the spatial schema for the multiplication process (see spatial acalculia).

Back to Main Page