

Apple Computer introduced the iMac computer in August 1998. The initial demand for the iMac was very high and Apple sold as many iMacs as they could make. One issue of great concern to Apple was whether the iMac attracting new customers and therefore expanding the base of Macintosh users or was only being bought by old customers who already owned a Macintosh.
To investigate, ComputerWare asked 500 of its iMac purchasers what computer they owned or had owned. There were 83 new computer owners, 60 who had owned a Windows-based computer, and 357 who had owned a Macintosh. The results are graphed below.
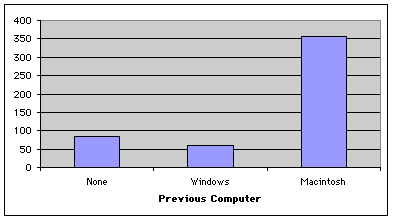
The proportion of first-time computer owners was 83/500 = 0.167. So, 0.167
is an estimate of the proportion of new computer owners. To determine the margin
of error, compute the 95% confidence interval
on the proportion. It extends from 0.13 to 0.20. Therefore, it is likely
that between 13% and 20% of iMac buyers are first-time computer owners.
Assumptions
The confidence interval on the proportion assumes that the sampling distribution of p is normal. The sampling distribution with N = 500 and the true portion (Pi) being 0.1667 can be found using the "Normal Approximation to the Binomial" demonstration. The effect of any violation on the confidence interval can be tested using the "Confidence interval on Pi" demonstration.
A second assumption is that each observation (customer) is independent
of each other observation. There is no reason to suppose this assumption is
violated.
Epilog
After one year and the sale of 2,000,000 iMacs, Apple reports that one third of the new buyers of iMacs are first-time computer buyers. This is outside the 95% confidence interval that runs extends from 0.13 to 0.20. Is this sampling error or might there be other factors at work here?