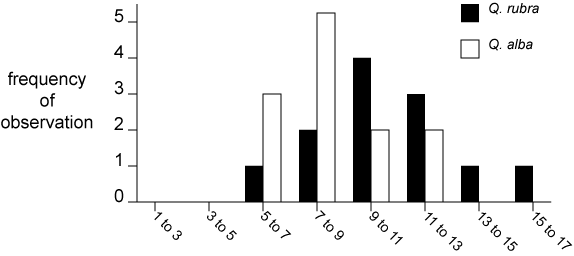
Your plot should now look something like this.
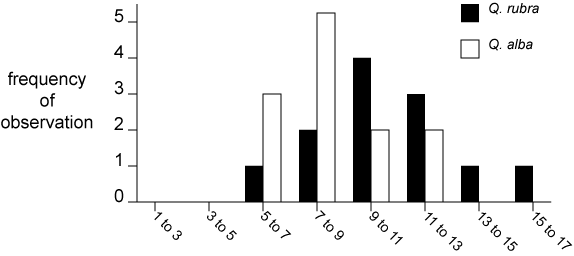
| Quercus rubra | 5-7 | 7-9 | 9-11 | 7-9 | 9-11 | 9-11 | 11-13 | 11-13 | 9-11 | 11-13 | 13-15 | 15-17 |
| Quercus alba | 11-13 | 9-11 | 5-7 | 9-11 | 11-13 | 7-9 | 7-9 | 7-9 | 5-7 | 7-9 | 7-9 | 5-7 |
The data are now beginning to resemble what we call a normal distribution. In a normal distribution the collected data are distributed predictably about a central mean. Now 12 is considered to be a rather small number of data points, particularly when they are scattered like this. You can see a difference in the central tendency of the two data sets, but is it significant? To test for a significant difference we have to work with what we call a theoretical distribution. A theoretical distribution extrapolates the sample data to the case in which the number of data points n approaches infinity and the width of each category approaches zero. For normally distributed data the theoretical distribution resembles a bell curve.
Now sketch two bell curves over your graph. Match what you think would be the full range of the data, make each curve symmetrical, and put the peaks about where the mean values fell. Recall that the mean values were 10.6 ± 2.9 cm for Quercus rubra and 8.2 ± 2.0 cm for Quercus alba. You don't need to place the columns entirely inside each curve. You might want to use solid and dashed lines to distinguish the curves.